题目内容
21、如图①，将矩形ABCD沿着对角线AC分割，得到△ABC和△ACD，将△ACD绕点A按逆时针方向旋转α度，使D，A，B三点在同一直线上，得到图②，再把图②中的△ADE沿着AB方向平移s格，使点D与点A重合，得到图③，设EF与AC相交于点G．
请解答以下问题：
（1）上述过程中，α=
（2）在图③中，除了△ABC∽△EAF以外，还能找出对相似三角形；
（3）请写一对你在图③中找出的相似三角形，并加以证明．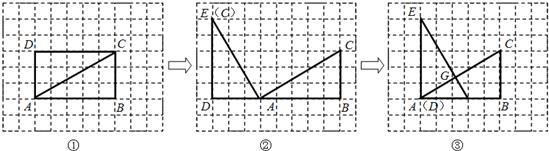
请解答以下问题：
（1）上述过程中，α=
90
度，s=3
格；（2）在图③中，除了△ABC∽△EAF以外，还能找出对相似三角形；
（3）请写一对你在图③中找出的相似三角形，并加以证明．
分析：（1）根据已知及图形分析容易得出；
（2）根据相似三角形的判定即可找到存在的相似三角形；
（3）从（2）中找出一对，根据相似三角形的判定方法，结合旋转、平移的性质，进行证明．
（2）根据相似三角形的判定即可找到存在的相似三角形；
（3）从（2）中找出一对，根据相似三角形的判定方法，结合旋转、平移的性质，进行证明．
解答：解：（1）根据图形分析容易得出：α=90°，S=3．（4分）
（2））△AEF∽△GAF；△AEF∽△ABC；△ABC∽△GAF；△GAE∽△ABC；△GAE∽△AGF共5对．（6分）
（3）△AEF∽△GAF．（7分）
证明：∵在图①中，四边形ABCD是矩形
∴∠ACD=∠CAB
即在图③中，∠AEF=∠GAF（8分）
又∵∠AFE=∠GFA（9分）
∴△AEF∽△GAF（10分）
（2））△AEF∽△GAF；△AEF∽△ABC；△ABC∽△GAF；△GAE∽△ABC；△GAE∽△AGF共5对．（6分）
（3）△AEF∽△GAF．（7分）
证明：∵在图①中，四边形ABCD是矩形
∴∠ACD=∠CAB
即在图③中，∠AEF=∠GAF（8分）
又∵∠AFE=∠GFA（9分）
∴△AEF∽△GAF（10分）
点评：本题主要考查相似三角形的判定方法及平移、旋转的性质等的综合运用．
练习册系列答案
阅读快车系列答案
相关题目
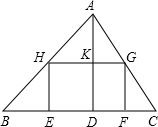如图所示，某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造．已知△ABC的边BC长120米，高AD长80米．学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分（如图）．其中矩形EFGH的一边EF在边BC上．其中两个顶点H、G分别在边AB、AC上．现计划在△AHG上种草，在△BHE、△GFC上都种花，在矩形EFGH上兴建喷泉．当FG长为多少米时，种草的面积与种花的面积相等？
时，求出y的值；
