题目内容
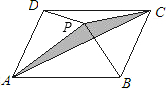如图，P是平行四边形ABCD内一点，且S△PAB=5，S△PAD=2，则阴影部分的面积为________．
3
分析：可由S△PAB+S△PCD=
S?ABCD=S△ACD，再通过面积之间的转化，进而得出结论．
解答：∵S△PAB+S△PCD=S?ABCD=S△ACD，
∴S△ACD-S△PCD=S△PAB，
则S△PAC=S△ACD-S△PCD-S△PAD，
=S△PAB-S△PAD，
=5-2，
=3．
故答案为：3．
点评：本题主要考查平行四边形内三角形面积的求解问题，应熟练掌握此类问题．
分析：可由S△PAB+S△PCD=
S?ABCD=S△ACD，再通过面积之间的转化，进而得出结论．解答：∵S△PAB+S△PCD=
S?ABCD=S△ACD，∴S△ACD-S△PCD=S△PAB，
则S△PAC=S△ACD-S△PCD-S△PAD，
=S△PAB-S△PAD，
=5-2，
=3．
故答案为：3．
点评：本题主要考查平行四边形内三角形面积的求解问题，应熟练掌握此类问题．
练习册系列答案
名校课堂系列答案
相关题目
22、如图，E是平行四边形ABCD的边BA延长线上一点，连接EC，交AD于F．
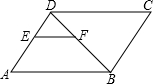如图，E是平行四边形ABCD的AD边上一点，过点E作EF∥AB交BD于F，若DE：EA=2：3，EF=4，则CD的长为（ ）A、
| ||
| B、8 | ||
| C、10 | ||
| D、16 |
（2012•黄埔区一模）如图，AC是平行四边形ABCD的对角线，∠ACB=∠ACD．
（2012•荆州模拟）如图，G是平行四边形ABCD的边CD延长线上一点，BG交AC于E，交AD于F，则图中与△FGD相似的三角形有（ ）
如图，ABCD是平行四边形，∠DAB=α，AC是对角线．△ADC绕点A旋转β度角，得到△AD′C′，连结D′B．若△ABC≌△BAD′，试求出α与β的关系．