题目内容
如下图,已知△ABC与△CDA关于点O中心对称,过O作直线EF分别交AD、BC于点EF,下面的结论:
①点E和点F,点B和点D是关于中心O的对称点;
②直线BD必经过点O;
③四边形ABCD是中心对称图形;
④四边形DEOC与四边形BFOA的面积必相等;
⑤△AOE与△COF成中心对称.其中正确的个数为
[ ]
A.2
B.3
C.4
D.5

答案:D
解析:
提示:
解析:
|
△ABC与△CDA关于点O对称是两个图形的关系,但如果把这两个图形看成一个整体,即为四边形ABCD,那么四边形ABCD就是一个关于点O的中心对称图形,故③正确;B与D关于点O成中心对称,这两点就是对称点,同时对称点的连线必经过对称中心,故①②都正确;由中心对称图形的性质得知,四边形DEOC与四边形BFOA是四对对称点所围成的图形,△AOE与△COF也是对称点所围成的图形,所以它们分别成中心对称,故④和⑤都正确. |
提示:
|
本题结合实际图形考查了中心对称与中心对称图形的概念、性质及相互关系,这是本节的一个难点.通过此类题目的训练,可以使学生从本质上理解中心对称与中心对称图形这两个概念. 把两个成中心对称的图形看成一个整体,即可转化为一个中心对称图形,这是成中心对称的图形与中心对称图形之间的辩证关系. |

练习册系列答案
相关题目
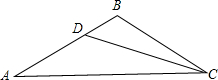 如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为
如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为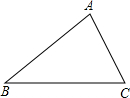 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹) 24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)