题目内容
【题目】某演唱会购买门票的方式有两种
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;(注方式一中总费用=广告费用+门票费用)
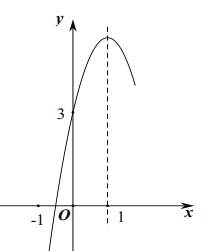
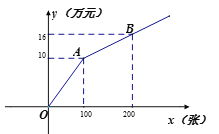
方式二:按如图所示的购买门票方式.
设购买门票x张,总费用为y万元.
(1)求按方式一购买时y与x的函数关系式
(2)若甲、乙两个单位分采用方式一,方式二购买本场演唱会门共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
【答案】(1)y=10+0.02x;(2)甲、乙两单位购买门票分别为270张和130张.
【解析】
(1)方案一中,总费用=广告费用10+门票单价0.02×票的张数;
(2)方案二中,当x≥100时,设出一次函数解析式,把其中两点的坐标代入即可求得相应的函数解析式;然后设乙单位购买了a张门票,则甲单位购买了(400a)张门票,根据两单位共花费27.2万元,列出方程解答即可.
解:(1)方案一:单位赞助广告费10万元,该单位所购门票的价格为每张0.02万元,
则y=10+0.02x;
(2)方案二:当x≥100时,设解析式为y=kx+b.
将(100,10),(200,16)代入,得 ![]() ,
,
解得![]() ,
,
所以y=0.06x+4.
设乙单位购买了a张门票,则甲单位购买了(400a)张门票,
根据题意得:0.06a+4+[10+0.02(400a)]=27.2,
解得:a=130,
∴400a=270,
答:甲、乙两单位购买门票分别为270张和130张.

 名校课堂系列答案
名校课堂系列答案【题目】为了调查A、B两个区的初三学生体育测试成绩,从两个区各随机抽取了1000名学生的成绩(满分:40分,个人成绩四舍五入向上取整数)
A区抽样学生体育测试成绩的平均分、中位数、众数如下:
平均分 | 中位数 | 众数 |
37 | 36 | 37 |
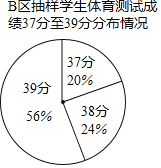
B区抽样学生体育测试成绩的分布如下:
成绩 | 28≤x<31 | 31≤x<34 | 34≤x<37 | 37≤x<40 | 40(满分) |
人数 | 60 | 80 | 140 | m | 220 |
请根据以上信息回答下列问题
(1)m= ;
(2)在两区抽样的学生中,体育测试成绩为37分的学生,在 (填“A”或“B”)区被抽样学生中排名更靠前,理由是 ;
(3)如果B区有10000名学生参加此次体育测试,估计成绩不低于34分的人数.