题目内容
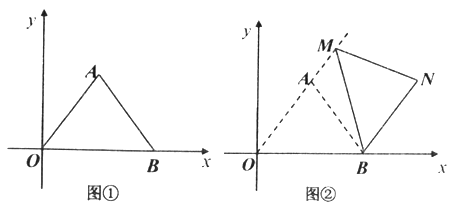
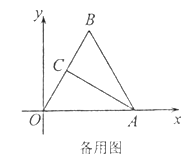
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且![]() 为等边三角形,C为OB的中点,连接AC.
为等边三角形,C为OB的中点,连接AC.
(I)如图①,求点C的坐标;
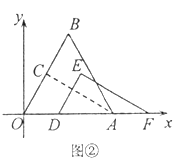
(I)如图②,将![]() 沿x轴向右平移得到
沿x轴向右平移得到![]() ,设
,设![]() ,其中
,其中![]()
①设![]() 与
与![]() 重叠部分的面积为S,用含m的式子表示S:
重叠部分的面积为S,用含m的式子表示S:
②连接![]() ,当
,当![]() 取最小值时,求点E的坐标(直接写出结果即可).
取最小值时,求点E的坐标(直接写出结果即可).
【答案】(I)点C的坐标为![]() ;(Ⅱ)①
;(Ⅱ)①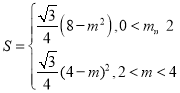 ;②
;②![]()
【解析】
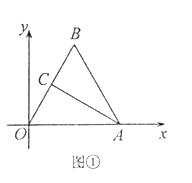
(1) 过C作![]() ,垂足为H.由
,垂足为H.由![]() 可求出CH,OH的长度,C点的坐标;
可求出CH,OH的长度,C点的坐标;
(2)①根据点E是否在△OAB内,重合的面积的形状不同进行分类求解;
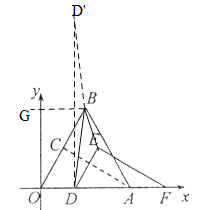
②作BG平行于x轴,作D点关于BG的对称点D’,连接D’B,则当D’,B,E三点共线时,线段和最小,可以表示出D’,B,E三点的坐标,并且共线求出m,即可求解.
解:(I)如图,过C作![]() ,垂足为H.
,垂足为H.
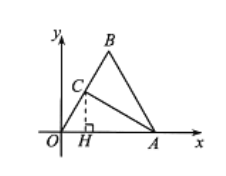
![]() 为等边三角形,
为等边三角形,
![]()
∵C为OB的中点,![]()
![]()
∴点C的坐标为![]()
(Ⅱ)①![]() 是
是![]() 平移得到的,
平移得到的,![]()
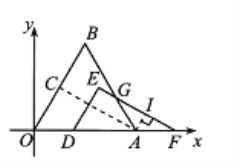
当![]() 时,如图,设AB与EF交于点G,
时,如图,设AB与EF交于点G,
过点A作![]() ,垂足为I.
,垂足为I.
![]()
![]()
![]() .
.
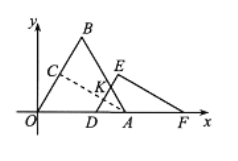
当![]() 时,如图,设AB与DE交于点K,
时,如图,设AB与DE交于点K,
![]()
综上所述,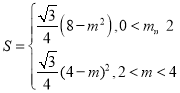
②作BG平行于x轴,作D点关于BG的对称点D’,连接D’B, 当D’,B,E三点共线时,线段和最小,
D(m,0), B(2,![]() ), D’(m,
), D’(m,![]() ),E(m+1,
),E(m+1,![]() )
)
设三点共线的直线方程为y=kx+b,代入得
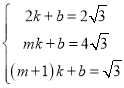 解得
解得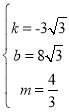
∴E![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
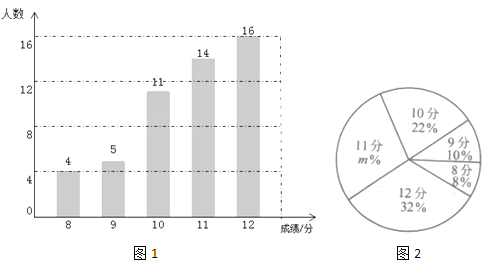
小学生10分钟应用题系列答案【题目】为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
组别 | 成绩x | 组中值 | 频数 |
第一组 | 90≤x≤100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | |
第三组 | 70≤x<80 | 75 | 8 |
第四组 | 60≤x<70 | 65 |
观察图表信息,回答下列问题:
(1)参赛教师共有 人;
(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩;
(3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.