题目内容
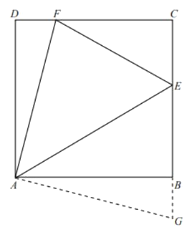
【题目】如图①,在正方形ABCD中,![]() ,点E,F分别在BC、CD上,
,点E,F分别在BC、CD上,![]() ,试探究
,试探究![]() 面积的最小值。
面积的最小值。
下面是小丽的探究过程:
(1)延长EB至G,使![]() ,连接AG,可以证明
,连接AG,可以证明![]() .请完成她的证明;
.请完成她的证明;
(2)设![]() ,
,![]() ,
,![]()
①结合(1)中结论,通过计算得到![]() 与x的部分对应值。请求出表格中a的值:(写出解答过程)
与x的部分对应值。请求出表格中a的值:(写出解答过程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的结论通过描点、连线可以分别画出函数![]() 、
、![]() 的图像、请在图②中完善她的画图;
的图像、请在图②中完善她的画图;
③根据以上探究,估计![]() 面积的最小值约为(结果估计到0.1)。
面积的最小值约为(结果估计到0.1)。


图① 图②
【答案】(1)见解析;(2)①![]() ,②见解析;③41.4或41.5.
,②见解析;③41.4或41.5.
【解析】
(1)AB=AD,BG=DF,则AG=AF,∠DAF+∠BAE=90°-∠EAF=45°=∠EAF,AF=AG,AE=AE,则△AFE≌△AGE(SAS),即可求解;
(2)①∵CE=BC-6=4,设DF=a,CF=10-a,EF=DF+BE=6+a,由勾股定理即可求解;②由①得:y2=y1+x,描点画图即可;
(3)利用分割法即可得出.
(1)证明:如图①,延长EB至G,使![]() ,连接AG.
,连接AG.
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)①在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解这个方程,得![]() .
.
②如图②所示.
③S△AEF=S![]() ABCD- S△ADF - S△ABE - S△EFC
ABCD- S△ADF - S△ABE - S△EFC
=100-![]()
![]() -
-![]() -
-![]()
=100-![]() (DF+BE)
(DF+BE)![]() 10-
10-![]()
=100-![]()
![]() EF
EF![]() 10-
10-![]()
=100-5y2-![]() (10-x)(10-y1)
(10-x)(10-y1)
=50-![]() xy1
xy1
当x=4,y1=4.29时,S△AEF最小
S△AEF=50-![]() ×4×.29≈41.4或41.5.
×4×.29≈41.4或41.5.

图① 图②

练习册系列答案
相关题目