题目内容
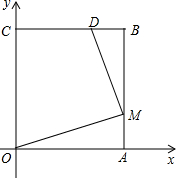 在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B的坐标为(5,6),点M在AB边上,且BM=5AM,连接OM,作MD⊥OM交BC于点D.
在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B的坐标为(5,6),点M在AB边上,且BM=5AM,连接OM,作MD⊥OM交BC于点D.(1)求证:OM=DM;
(2)求直线MD的函数关系式;
(3)若点M在线段AB上运动(不与点A,B重合)且始终保持MD⊥OM(点D在BC上),
①设点D的横坐标为a,求a的最小值及此时点M的坐标;
②点N也是线段AB上的一个动点,点N与点M不重合,连接ON、DN时,也有DN⊥ON.设BN=n,BM=m,直接写出n与m的函数表达式,并写出自变量m的取值范围.
分析:(1)首先求得MB的长,然后证明∠OMA=∠BDM,利用AAS即可证得△OAM≌△MBD,根据全等三角形的对应边相等证得;
(2)首先求得D,M的坐标,然后利用待定系数法即可求得函数的解析式;
(3)①首先证明△OAM∽△MBD,设M的坐标是(5,x),根据相似三角形的对应边的比相等即可得到x于a的函数关系式,然后利用二次函数的性质即可求解;
②6-m和6-n都是方程a=
x2-
x+6的根,利用根与系数的关系即可求得.
(2)首先求得D,M的坐标,然后利用待定系数法即可求得函数的解析式;
(3)①首先证明△OAM∽△MBD,设M的坐标是(5,x),根据相似三角形的对应边的比相等即可得到x于a的函数关系式,然后利用二次函数的性质即可求解;
②6-m和6-n都是方程a=
| 1 |
| 5 |
| 6 |
| 5 |
解答:解:(1)证明:∵点B的坐标为(5,6),
∴OA=BC=5,AB=OC=6,
∵BM=5AM,
∴BM=5,AM=1,
∴BM=OA,
∵MD⊥OM,
∴∠DMB=∠OMA=90°,
又∵∠B=90°,
∴∠DMB+∠BDM=90°,
∴∠OMA=∠BDM,
在△OAM和△MBD中,
,
∴△OAM≌△MBD;
∴OM=DM;
(2)∵△OAM≌△MBD,
∴BD=AM=1,
则M的坐标是(5,1),D的坐标是(4,6),
设直线MD的函数关系式是y=kx+b,
则
,
解得:
,
则函数的解析式是:y=-5x+26;
(3)①设M的坐标是(5,x),
∵在△OAM和△MBD,∠OMA=∠BDM,∠B=∠OAM,
∴△OAM∽△MBD,
∴
=
,即
=
,
解得:a=
x2-
x+6,
则当x=3时a有最小值是:
×9-
×3+6=
;
M的坐标是(5,3);
②∵点N与点M不重合,连接ON、DN时,也有DN⊥ON,
∴6-m和6-n都是方程a=
x2-
x+6的根,
∴6-m+(6-n)=3,则m+n=9.
即n=9-m(0<m<6).

∴OA=BC=5,AB=OC=6,
∵BM=5AM,
∴BM=5,AM=1,
∴BM=OA,
∵MD⊥OM,
∴∠DMB=∠OMA=90°,
又∵∠B=90°,
∴∠DMB+∠BDM=90°,
∴∠OMA=∠BDM,
在△OAM和△MBD中,
|
∴△OAM≌△MBD;
∴OM=DM;
(2)∵△OAM≌△MBD,
∴BD=AM=1,
则M的坐标是(5,1),D的坐标是(4,6),
设直线MD的函数关系式是y=kx+b,
则
|
解得:
|
则函数的解析式是:y=-5x+26;
(3)①设M的坐标是(5,x),
∵在△OAM和△MBD,∠OMA=∠BDM,∠B=∠OAM,
∴△OAM∽△MBD,
∴
| OA |
| BM |
| AM |
| BD |
| 5 |
| 6-x |
| x |
| 6-a |
解得:a=
| 1 |
| 5 |
| 6 |
| 5 |
则当x=3时a有最小值是:
| 1 |
| 5 |
| 6 |
| 5 |
| 21 |
| 5 |
M的坐标是(5,3);
②∵点N与点M不重合,连接ON、DN时,也有DN⊥ON,
∴6-m和6-n都是方程a=
| 1 |
| 5 |
| 6 |
| 5 |
∴6-m+(6-n)=3,则m+n=9.
即n=9-m(0<m<6).
点评:本题是全等三角形的判定与性质,待定系数法求函数的解析式,以及一元二次方程的根与系数的关系的综合应用,正确求得x于a的函数关系式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.