题目内容
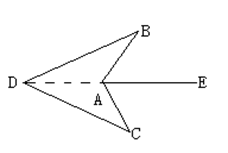
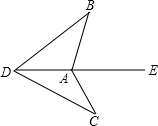如图，AE是∠BAC的平分线，AB=AC，D是AE反向延长线的一点，则△ABD与△ACD全等吗？为什么？
分析：依据题中有条件AB=AC，隐含AD=AD，再证明出∠DAB=∠DAC，从而利用SAS来证明两个三角形全等．
解答：解：∵AE是∠BAC的平分线，
∴∠BAE=∠CAE；
∴180°-∠BAE=180°-∠CAE，
即∠DAB=∠DAC；
又∵AB=AC，AD=AD，
∴在△ABD和△ACD中，
∴△ABD≌△ACD（SAS）．
∴∠BAE=∠CAE；
∴180°-∠BAE=180°-∠CAE，
即∠DAB=∠DAC；
又∵AB=AC，AD=AD，
∴在△ABD和△ACD中，
|
∴△ABD≌△ACD（SAS）．
点评：本题主要考查等角的补角相等，SAS的判定定理．题目比较简单．
练习册系列答案
阅读快车系列答案
相关题目
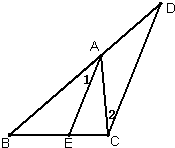26、已知，如图，AE是∠BAC的平分线，∠1=∠D．
5、如图，AE是∠BAC的平分线，AB=AC．
