题目内容
如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
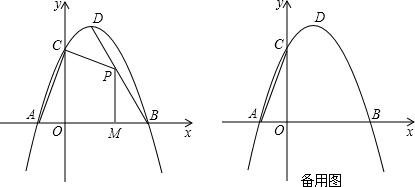
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标.

(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为
(2,3)
(2,3)
时,四边形PQAC是平行四边形 (利用备用图画图,直接写出结果,不写求解过程);(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标.
分析:(1)已知抛物线与x轴的两个交点,可将二次函数的解析式设为交点式,再代入C点的坐标即可,进而能得出顶点D的坐标.
(2)已知PQ∥AC,若四边形PQAC是平行四边形,那么CP必与AQ平行,即CP与x轴平行,因此点C、P关于抛物线对称轴对称,则P点坐标可得.
(3)四边形PMAC是个不规则的图形,可以将它的面积分成两部分:梯形PMOC、△AOC,首先利用待定系数法求出直线BD的解析式,然后设出点P的坐标,进而能用未知数表达出PM、OC、OM的长,再根据上面得出的图形间的面积和差关系求出关于四边形PMAC的面积与点P横坐标的函数关系式,根据函数的性质即可得出四边形PMAC的最大面积以及对应的P点的坐标.
(2)已知PQ∥AC,若四边形PQAC是平行四边形,那么CP必与AQ平行,即CP与x轴平行,因此点C、P关于抛物线对称轴对称,则P点坐标可得.
(3)四边形PMAC是个不规则的图形,可以将它的面积分成两部分:梯形PMOC、△AOC,首先利用待定系数法求出直线BD的解析式,然后设出点P的坐标,进而能用未知数表达出PM、OC、OM的长,再根据上面得出的图形间的面积和差关系求出关于四边形PMAC的面积与点P横坐标的函数关系式,根据函数的性质即可得出四边形PMAC的最大面积以及对应的P点的坐标.
解答:解:(1)依题意,设抛物线的解析式:y=a(x+1)(x-3),代入C(0,3),得:
3=a(0+1)(0-3),解得:a=-1
∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.抛物线顶点D的坐标为(1,4).
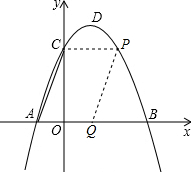 (2)已知PQ∥AC,若四边形PMAC是平行四边形,必有CP∥AQ,即CP∥x轴;(如右图)
(2)已知PQ∥AC,若四边形PMAC是平行四边形,必有CP∥AQ,即CP∥x轴;(如右图)
∴点C、P关于抛物线的对称轴对称;
已知C(0,3),抛物线对称轴x=1,则P(2,3).
(3)设直线BD的解析式为y=kx+b,
由B(3,0),D(1,4)得
,解得
;
∴直线BD的解析式为y=-2x+6.
∵点P在直线PD上,∴设P(p,-2p+6).
则OA=1,OC=3,OM=p,PM=-2p+6.
∴S四边形PMAC=S△OAC+S梯形OMPC=
•1•3+
•(3-2p+6)•p=-p2+
p+
=-(p-
)2+
.
∵1<
<3,∴当p=
时,四边形PMAC的面积取得最大值为
,此时点P的坐标为(
,
).
3=a(0+1)(0-3),解得:a=-1
∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.抛物线顶点D的坐标为(1,4).
 (2)已知PQ∥AC,若四边形PMAC是平行四边形,必有CP∥AQ,即CP∥x轴;(如右图)
(2)已知PQ∥AC,若四边形PMAC是平行四边形,必有CP∥AQ,即CP∥x轴;(如右图)∴点C、P关于抛物线的对称轴对称;
已知C(0,3),抛物线对称轴x=1,则P(2,3).
(3)设直线BD的解析式为y=kx+b,
由B(3,0),D(1,4)得
|
|
∴直线BD的解析式为y=-2x+6.
∵点P在直线PD上,∴设P(p,-2p+6).
则OA=1,OC=3,OM=p,PM=-2p+6.
∴S四边形PMAC=S△OAC+S梯形OMPC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 105 |
| 16 |
∵1<
| 9 |
| 4 |
| 9 |
| 4 |
| 105 |
| 16 |
| 9 |
| 4 |
| 3 |
| 2 |
点评:此题主要考查了利用待定系数法求二次函数的解析式、平行四边形的判定和性质以及图形面积的求法,解题时要注重数形结合,难度适中.

练习册系列答案
相关题目
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC. 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).