Question

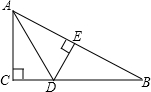如图，Rt△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，下列结论错误的是

1. A.
   BD+DE=BC
2. B.
   DE平分∠ADB
3. C.
   AD平分∠EDC
4. D.
   AC+DE＞AD

Answer 1

B
分析：观察已知条件，由角平分线的性质可得CD=DE，进而可得更多的结论，然后对各选项进行验证、证明可得答案．
解答：A、∵CD=DE，
∴BD+DE=BC
所以A是正确结论；
B、缺少条件，不能得出，所以B是错误结论；
C、∴AC=AE
又有AD=AD，
可证△AED≌△ACD
∴∠ADE=∠ADC
即AD平分∠EDC；
所以C是正确结论；
D、在△ACD中，CD+AC＞AD
所以ED+AC＞AD．所以D是正确结论．
故本题选B．
点评：本题主要考查平分线的性质，由已知能够注意到△AED≌△ACD是解决的关键．