题目内容
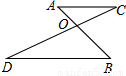
如图所示,BO、CD分别平分∠ABC 和∠ACB。
(1)若∠A=60°,求∠O;
(2)若∠A=80°、120°,∠O是多少度?
(3)由(1)、(2)你发现了什么规律?请用数学式子写出你发现的规律。(提示:三角形的三个内角度数之和为180°)
(1)若∠A=60°,求∠O;
(2)若∠A=80°、120°,∠O是多少度?
(3)由(1)、(2)你发现了什么规律?请用数学式子写出你发现的规律。(提示:三角形的三个内角度数之和为180°)

解:(1)因为∠A=60°,
所以∠ABC+∠ACB=180°-60°=120°,
而BO、CD分别平分∠ABC、∠ACB,
所以∠OBC+
所以∠O=180°-(∠OBC+∠OCB)=180°-60°=120°;
(2)同理可得:当∠A= 80°时,∠O=13°;
当∠A=120°时,∠O=150°;
(3)由(1)(2)可知:∠ 。
。
所以∠ABC+∠ACB=180°-60°=120°,
而BO、CD分别平分∠ABC、∠ACB,
所以∠OBC+

所以∠O=180°-(∠OBC+∠OCB)=180°-60°=120°;
(2)同理可得:当∠A= 80°时,∠O=13°;
当∠A=120°时,∠O=150°;
(3)由(1)(2)可知:∠
 。
。 
练习册系列答案
相关题目
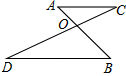 如图所示,AB、CD相交于点O,AO=2,BO=4,CO=3,DO=6,
如图所示,AB、CD相交于点O,AO=2,BO=4,CO=3,DO=6, 如图所示,AB与CD相交于点O,且AO=BO,CO=DO,过点O作直线EF交AC于E,交BD于F,试说明OE=OF.
如图所示,AB与CD相交于点O,且AO=BO,CO=DO,过点O作直线EF交AC于E,交BD于F,试说明OE=OF.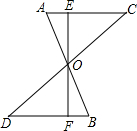 如图所示,AB与CD相交于点O,且AO=BO,CO=DO,过点O作直线EF交AC于E,交BD于F,试说明OE=OF.
如图所示,AB与CD相交于点O,且AO=BO,CO=DO,过点O作直线EF交AC于E,交BD于F,试说明OE=OF.