题目内容
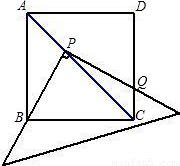
(2009•通州区二模)如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.
(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.
【答案】分析:(1)PQ=PB,过P点作MN∥BC分别交AB、DC于点M、N,可以证明Rt△MBP≌Rt△NPQ;
(2)S四边形PBCQ=S△PBC+S△PCQ分别表示出△PBC于△PCQ的面积就可以.
(3)△PCQ可能成为等腰三角形.①当点P与点A重合时,点Q与点D重合,PQ=QC,
②当点Q在DC的延长线上,且CP=CQ时,就可以用x表示出面积.
解答:解:(1)PQ=PB,(1分)
过P点作MN∥BC分别交AB、DC于点M、N,
在正方形ABCD中,AC为对角线,
∴AM=PM,
又∵AB=MN,
∴MB=PN,
∵∠BPQ=90°,
∴∠BPM+∠NPQ=90°;
又∵∠MBP+∠BPM=90°,
∴∠MBP=∠NPQ,
在Rt△MBP≌Rt△NPQ中,
∵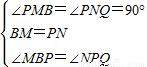
∴Rt△MBP≌Rt△NPQ,(2分)
∴PB=PQ.
(2)∵S四边形PBCQ=S△PBC+S△PCQ,
∵AP=x,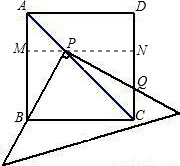
∴AM=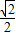 x,
x,
∴CQ=CD-2NQ=1- x,
x,
又∵S△PBC= BC•BM=
BC•BM= •1•(1-
•1•(1-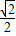 x)=
x)= -
-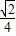 x,
x,
S△PCQ= CQ•PN=
CQ•PN= (1-
(1-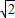 x)•(1-
x)•(1-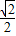 x),
x),
=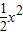 -
-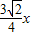 +
+ ,
,
∴S四边形PBCQ=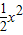 -
-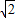 x+1.(0≤x≤
x+1.(0≤x≤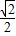 ).(4分)
).(4分)

(3)△PCQ可能成为等腰三角形.
①当点P与点A重合时,点Q与点D重合,
PQ=QC,此时,x=0.(5分)
②当点Q在DC的延长线上,且CP=CQ时,(6分)
有:QN=AM=PM=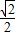 x,CP=
x,CP=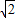 -x,CN=
-x,CN=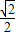 CP=1-
CP=1-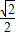 x,CQ=QN-CN=
x,CQ=QN-CN=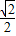 x-(1-
x-(1-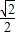 x)=
x)=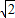 x-1,
x-1,
∴当 -x=
-x=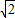 x-1时,x=1.(7分).
x-1时,x=1.(7分).
点评:此题主要考查正方形及直角三角形的性质及全等三角形的判定方法的综合运用.
(2)S四边形PBCQ=S△PBC+S△PCQ分别表示出△PBC于△PCQ的面积就可以.
(3)△PCQ可能成为等腰三角形.①当点P与点A重合时,点Q与点D重合,PQ=QC,
②当点Q在DC的延长线上,且CP=CQ时,就可以用x表示出面积.
解答:解:(1)PQ=PB,(1分)
过P点作MN∥BC分别交AB、DC于点M、N,
在正方形ABCD中,AC为对角线,
∴AM=PM,
又∵AB=MN,
∴MB=PN,
∵∠BPQ=90°,
∴∠BPM+∠NPQ=90°;
又∵∠MBP+∠BPM=90°,
∴∠MBP=∠NPQ,
在Rt△MBP≌Rt△NPQ中,
∵
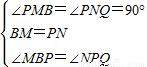
∴Rt△MBP≌Rt△NPQ,(2分)
∴PB=PQ.
(2)∵S四边形PBCQ=S△PBC+S△PCQ,
∵AP=x,

∴AM=
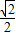 x,
x,∴CQ=CD-2NQ=1-
 x,
x,又∵S△PBC=
 BC•BM=
BC•BM= •1•(1-
•1•(1-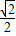 x)=
x)= -
-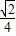 x,
x,S△PCQ=
 CQ•PN=
CQ•PN= (1-
(1-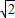 x)•(1-
x)•(1-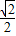 x),
x),=
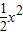 -
-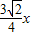 +
+ ,
,∴S四边形PBCQ=
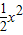 -
-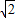 x+1.(0≤x≤
x+1.(0≤x≤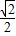 ).(4分)
).(4分)
(3)△PCQ可能成为等腰三角形.
①当点P与点A重合时,点Q与点D重合,
PQ=QC,此时,x=0.(5分)
②当点Q在DC的延长线上,且CP=CQ时,(6分)
有:QN=AM=PM=
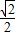 x,CP=
x,CP=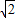 -x,CN=
-x,CN=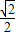 CP=1-
CP=1-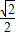 x,CQ=QN-CN=
x,CQ=QN-CN=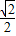 x-(1-
x-(1-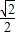 x)=
x)=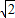 x-1,
x-1,∴当
 -x=
-x=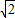 x-1时,x=1.(7分).
x-1时,x=1.(7分).点评:此题主要考查正方形及直角三角形的性质及全等三角形的判定方法的综合运用.

练习册系列答案
相关题目
 =c+
=c+ 的解是x1=c,x2=
的解是x1=c,x2= ;
; =c-
=c- (即x+
(即x+ =c+
=c+ )的解是x1=c,x2=-
)的解是x1=c,x2=- ;x+
;x+ =c+
=c+ 的解是:x1=c,x2=
的解是:x1=c,x2= ,…
,… =c+
=c+ (m≠0)的解,并利用“方程的解”的概念进行验证;
(m≠0)的解,并利用“方程的解”的概念进行验证; =a+
=a+ 的解吗?若能,请求出此方程的解;若不能,请说明理由.
的解吗?若能,请求出此方程的解;若不能,请说明理由. 的值.
的值.