题目内容
如图,在18×13的网格中每个小正方形的边长都是1.△ABC与△A′B′ C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.
C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.(1)在图中画出位似图形点O;(要保留画图痕迹)
(2)△ABC与△A′B′C′的位似比是
(3)请在此网格中,以点C为位似中心,再画一个△A1B1C,使它与△ABC的位似比等于2:1.
分析:(1)将对应点连接,并延长使其交于一点即为O点;
(2)根据三角形对应变的比值位似比,求出对应边的比值即可;
(3)根据它与△ABC的位似比等于2:1,将三角形扩大2倍即可,对应点相交于一点.
(2)根据三角形对应变的比值位似比,求出对应边的比值即可;
(3)根据它与△ABC的位似比等于2:1,将三角形扩大2倍即可,对应点相交于一点.
解答:解:(1)如图所示:
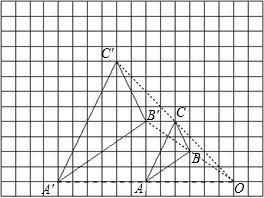 ;
;
(2)∵B′C′=2
,BC=
,
∴
=
=
,
∴△ABC与△A′B′C′的位似比是:1:2;
(3)如图所示:
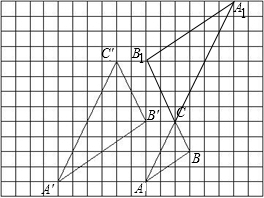 .
.
 ;
;(2)∵B′C′=2
| 5 |
| 5 |
∴
| BC |
| B′C′ |
| ||
2
|
| 1 |
| 2 |
∴△ABC与△A′B′C′的位似比是:1:2;
(3)如图所示:
 .
.点评:此题考查了找位似中心以及画位似图形.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目
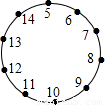
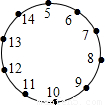
 23、10个人围成一圈每人想一个自然数,并告诉在他两边的人,然后每人将他两边的人告诉他的数的平均数报出来,报的结果如图,则报13的人心想的数是( )
23、10个人围成一圈每人想一个自然数,并告诉在他两边的人,然后每人将他两边的人告诉他的数的平均数报出来,报的结果如图,则报13的人心想的数是( )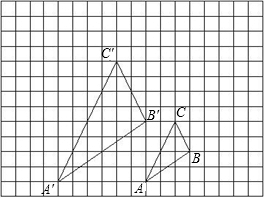 C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.
C′是关于点O为位似中心的位似图形,他们的顶点都在小正形的顶点上.