题目内容
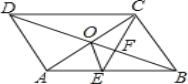
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°,②SABCD=ACBC;③OE:AC=![]() :6;④S△OCF=2S△OEF,⑤△OEF∽△BCF成立的个数有( )
:6;④S△OCF=2S△OEF,⑤△OEF∽△BCF成立的个数有( )
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据角平分线的定义得到∠DCE=∠BCE=60°推出△CBE是等边三角形,证得∠ACB=90°,求出∠ACD=∠CAB=30°,故①正确;由AC⊥BC,得到SABCD=ACBC,故②正确,根据直角三角形的性质得到AC=![]() BC,根据三角形的中位线的性质得到OE=
BC,根据三角形的中位线的性质得到OE=![]() BC,于是得到OE:AC=
BC,于是得到OE:AC=![]() :6,故③正确;由三角形的中位线可得BC∥OE,可判断△OEF∽△BCF,故⑤正确;根据相似三角形的性质得到
:6,故③正确;由三角形的中位线可得BC∥OE,可判断△OEF∽△BCF,故⑤正确;根据相似三角形的性质得到![]() =2,求得S△OCF=2S△OEF;故④正确.
=2,求得S△OCF=2S△OEF;故④正确.
解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
∵AC⊥BC,
∴SABCD=ACBC,故②正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=![]() BC,
BC,
∵AO=OC,AE=BE,
∴OE=![]() BC,
BC,
∴OE:AC=![]() :6;故③正确;
:6;故③正确;
∵AO=OC,AE=BE,
∴OE∥BC,
∴△OEF∽△BCF,故⑤正确;
∴![]() =2
=2
∴S△OCF:S△OEF=![]() =2,
=2,
∴S△OCF=2S△OEF;故④正确.
故选:D.

【题目】某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分.
学 生 类 型 人数 时间 |
|
|
|
|
| |
性别 | 男 | 7 | 31 | 25 | 30 | 4 |
女 | 8 | 29 | 26 | 32 | 8 | |
学段 | 初中 | 25 | 36 | 44 | 11 | |
高中 | ||||||

下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5-25.5之间
②这200名学生参加公益劳动时间的中位数在20-30之间
③这200名学生中的初中生参加公益劳动时间的中位数一定在20-30之间
④这200名学生中的高中生参加公益劳动时间的中位数可能在20-30之间
所有合理推断的序号是( )
A. ①③B. ②④C. ①②③D. ①②③④