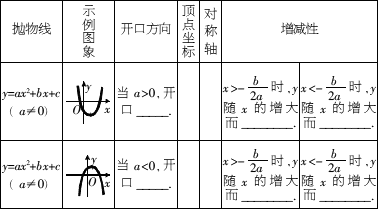
题目内容
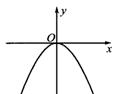
二次函数y=ax2的图像如图所示.

(1)求该函数的表达式.
(2)根据图像说明:x为何值时,y随x的增大而减小;x为何值时,y随x的增大而增大;x为何值时,函数y有最大值(或最小值).
(3)如果另有一函数y=![]() x2,它的图像与该函数的图像关于x轴对称、求另一函数的表达式.
x2,它的图像与该函数的图像关于x轴对称、求另一函数的表达式.
答案:
解析:
提示:
解析:
|
[答案](1)由已知,得3=( 故该函数表达式为y=x2. (2)x<0时,y随x的增大而减小;x>0时,y随x的增大而增大;x=0时,y有最小值0. (3)由题意知,另一函数的图像的对称轴也是y轴,顶点也是原点,则点A( 故-3=( [剖析]在讨论二次函数y=x2的性质时,需分x<0,x>0,x=0三种情况进行,必要时可结合其图像来加以分析.另外,两函数的图像关于x轴对称时,一个函数图像上的一点关于x轴的对称点必在另一函数的图像上. |
提示:
|
[方法提炼] 对于二次函数的性质,常常结合其图像,以其图像的对称轴为界分情况讨论. |

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目