题目内容
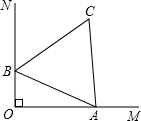 如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别在射线OM,ON上滑动,滑动过程中,连接OC,则OC的长的最大值是
如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别在射线OM,ON上滑动,滑动过程中,连接OC,则OC的长的最大值是1+
| 3 |
1+
.| 3 |
分析:取AB的中点D,连接OD及DC,根据三角形的边角关系得到OC小于等于OD+DC,只有当O、D及C共线时,OC取得最大值,最大值为OD+CD,由等边三角形的边长为2,根据D为AB中点,得到BD为1,根据三线合一得到CD垂直于AB,在直角三角形BCD中,根据勾股定理求出CD的长,在直角三角形AOB中,OD为斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半可得OD等于AB的一半,由AB的长求出OD的长,进而求出DC+OD,即为OC的最大值.
解答: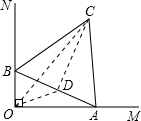 解:取AB中点D,连OD,DC,OC,有OC≤OD+DC,
解:取AB中点D,连OD,DC,OC,有OC≤OD+DC,
当O、D、C共线时,OC有最大值,最大值是OD+CD,
∵△ABC为等边三角形,D为中点,
∴BD=1,BC=2,根据勾股定理得:CD=
,
又△AOB为直角三角形,D为斜边AB的中点,
∴OD=
AB=1,
∴OD+CD=1+
,即OC的最大值为1+
.
故答案为:1+
 解:取AB中点D,连OD,DC,OC,有OC≤OD+DC,
解:取AB中点D,连OD,DC,OC,有OC≤OD+DC,当O、D、C共线时,OC有最大值,最大值是OD+CD,
∵△ABC为等边三角形,D为中点,
∴BD=1,BC=2,根据勾股定理得:CD=
| 3 |
又△AOB为直角三角形,D为斜边AB的中点,
∴OD=
| 1 |
| 2 |
∴OD+CD=1+
| 3 |
| 3 |
故答案为:1+
| 3 |
点评:此题考查了等边三角形的性质,直角三角形斜边上的中线等于斜边的一半,以及勾股定理,其中找出OC最大时的长为CD+OD是解本题的关键.

练习册系列答案
相关题目
 16、如图,OM⊥ON.已知正三角形ABC,两顶点A、B分别射线OM,ON上滑动,当∠OAB=21°时,∠NBC=
16、如图,OM⊥ON.已知正三角形ABC,两顶点A、B分别射线OM,ON上滑动,当∠OAB=21°时,∠NBC= 如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别向射线OM,ON上滑动,当∠OAB=21°时,∠NBC=
如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别向射线OM,ON上滑动,当∠OAB=21°时,∠NBC= 如图,OM⊥ON.已知正三角形ABC,两顶点A、B分别射线OM,ON上滑动,当∠OAB=21°时,∠NBC=________.
如图,OM⊥ON.已知正三角形ABC,两顶点A、B分别射线OM,ON上滑动,当∠OAB=21°时,∠NBC=________.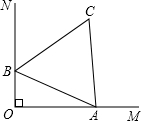 如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别在射线OM,ON上滑动,滑动过程中,连接OC,则OC的长的最大值是________.
如图,OM⊥ON.已知边长为2的正三角形ABC,两顶点A、B分别在射线OM,ON上滑动,滑动过程中,连接OC,则OC的长的最大值是________.