��Ŀ����
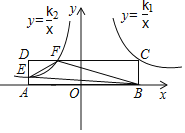
����Ŀ����֪��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ǵ�
�ֱ��ǵ�![]() ��
��![]() ��
��![]() �������϶�Ӧ����.
�������϶�Ӧ����.
��1�����![]() ���
���![]() �ľ��룻
�ľ��룻
��2�����ס�����������ֱ��![]() ��
��![]() ����ͬʱ�������������������˶������ǵ��ٶȷֱ���2��1����λ����/�룩���������ʱ���õ�ʱ�䣻
����ͬʱ�������������������˶������ǵ��ٶȷֱ���2��1����λ����/�룩���������ʱ���õ�ʱ�䣻
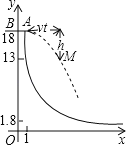
��3���ڣ�2���������£������������������˶����Ҷ��������Ḻ�����˶�.�����㿪ʼ�˶�ʱ����������4����λ����/����ٶȺͼ���ͬʱ�ӵ�![]() �������������˶����������������Ҷ���ʱ�������������Ḻ�����˶�������������ʱҲ���Ϸ��أ��������ֱ������������������ֹͣ�˶���������������ڵ�
�������������˶����������������Ҷ���ʱ�������������Ḻ�����˶�������������ʱҲ���Ϸ��أ��������ֱ������������������ֹͣ�˶���������������ڵ�![]() ����������ӿ�ʼ��ֹͣ�˶����������ߵ���·���Լ���
����������ӿ�ʼ��ֹͣ�˶����������ߵ���·���Լ���![]() ��Ӧ������.
��Ӧ������.
���𰸡���1��1����2��������ʱ���õ�ʱ��Ϊ6�룻��3���������˶�����·��Ϊ8����λ���ȣ���D��Ӧ������3.
��������
(1))���þ���ֵ�ķǸ��ԣ����a��b��c��ֵ,�����������뼴�ɣ�
(2)������ס�������������ٶȲ�ٸ���ʱ��=·�̡��ٶȼ��㼴������𰸣�
(3)���������������ʱ����Ҫ��ʱ�䣬��������˶�����·�̣������A�ߵ�·�̣������D��Ӧ��������.
�⣺��1����|a+1|��0����5��b��2��0��|c+2|��0�� |a+1|+��5��b��2+|c+2|��0��
��a+1��0��5��b��0��c+2��0��
��a����1��b��5��c����2��
��AC=��-1��-��-2��=1
��2�������⣬AB=5-��-1��=6
��6�£�2-1��=6
�𣺼�����ʱ���õ�ʱ��Ϊ6��.
��3���������⣬����������ʱ����Ҫ��ʱ��Ϊ
6�£�2+1��=2
��������˶�����·��Ϊ2��4��8����λ���ȣ�
�ߵ�A���ٶ�Ϊ2
���A�ߵ�·��Ϊ2��2=4
���D��Ӧ�����ǣ�-1��+4=3
�𣺱������˶�����·��Ϊ8����λ���ȣ���D��Ӧ������3.