题目内容
如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动.当其中一个动点到达端点时,另一个动点也随之 停止运动,两动点运动的时间t(s).
停止运动,两动点运动的时间t(s).
(1)当t为何值时,四边形MNBC是平行四边形;
(2)写出四边形ANMD的面积y(cm2)与t(s)的函数关系式,并画出函数的图象.
 停止运动,两动点运动的时间t(s).
停止运动,两动点运动的时间t(s).(1)当t为何值时,四边形MNBC是平行四边形;
(2)写出四边形ANMD的面积y(cm2)与t(s)的函数关系式,并画出函数的图象.
分析:(1)当四边形MNBC是平行四边形时,必须有CM=BN,而CM与BN均可用含有t的式子表示出来,所以列方程解答即可.
(2)要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义画出图象.
(2)要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义画出图象.
解答:解:∵运动时间为t秒,
∴DM=t(cm),CM=CD-DM=24-t(cm),BN=2t(cm),
(1)∵CD∥BA,
∴当MC=BN时,四边形MNBC是平行四边形.
此时有2t=24-t,解得t=8.
∴当t=8s时,四边形MNBC是平行四边形.
(2)∵在直角梯形ABCD中,DC∥AB,∠A=90,
∴四边形ANMD也是直角梯形,因此它的面积为
(DM+AN)×AD,∵DM=t,AN=28-2t,AD=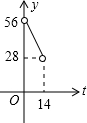 4;
4;
∴四边形AMND的面积y=
(t+28-2t)×4=-2t+56.
∵当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
∴当N点到达A点时,2t=28,t=14;
∴自变量t的取值范围是0<t<14.
故图象为:
∴DM=t(cm),CM=CD-DM=24-t(cm),BN=2t(cm),
(1)∵CD∥BA,
∴当MC=BN时,四边形MNBC是平行四边形.
此时有2t=24-t,解得t=8.
∴当t=8s时,四边形MNBC是平行四边形.
(2)∵在直角梯形ABCD中,DC∥AB,∠A=90,
∴四边形ANMD也是直角梯形,因此它的面积为
| 1 |
| 2 |
 4;
4;∴四边形AMND的面积y=
| 1 |
| 2 |
∵当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
∴当N点到达A点时,2t=28,t=14;
∴自变量t的取值范围是0<t<14.
故图象为:
点评:本题考查了平行四边形的判定、直角梯形的性质以及几何图形的性质确定函数的图象.此题难度较大,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.