题目内容
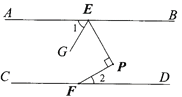
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
【答案】B
【解析】
延长EP交CD于点M,由三角形外角的性质可得∠FMP=90°-∠2,再根据平行线的性质可得∠BEP=∠FMP,继而根据平角定义以及∠BEP=∠GEP即可求得答案.
延长EP交CD于点M,
∵∠EPF是△FPM的外角,
∴∠2+∠FMP=∠EPF=90°,
∴∠FMP=90°-∠2,
∵AB//CD,
∴∠BEP=∠FMP,
∴∠BEP=90°-∠2,
∵∠1+∠BEP+∠GEP=180°,∠BEP=∠GEP,
∴∠1+90°-∠2+90°-∠2=180°,
∴∠1=2∠2,
故选B.


练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目










