题目内容
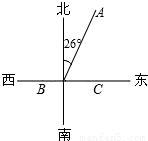
如图,A,B,C三个粮仓的位置如图所示,A粮仓在B粮仓北偏东26°,180千米处;C粮仓在B粮仓的正东方,A粮仓的正南方.已知A,B两个粮仓原有存粮共450吨,根据灾情需要,现从A粮仓运出该粮仓存粮的 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)(1)A,B两处粮仓原有存粮各多少吨?
(2)C粮仓至少需要支援200吨粮食,问此调拨计划能满足C粮仓的需求吗?
(3)由于气象条件恶劣,从B处出发到C处的车队来回都限速以每小时35公里的速度匀速行驶,而司机小王的汽车油箱的油量最多可行驶4小时,那么小王在途中是否需要加油才能安全地回到B地?请你说明理由.
【答案】分析:(1)由题意可知要求A,B两处粮仓原有存粮各多少吨需找等量关系,即A处存粮+B处存粮=450吨,A处存粮的五分之二=B处存粮的五分之三,据等量关系列方程组求解即可;
(2)分别求出A处和B处支援C处的粮食,将其加起来与200吨比较即可;
(3)由题意可知由已知可得△ABC中∠A=26°∠ACB=90°且AB=180Km,sin∠BAC= ,要求BC的长,可以运用三角函数解直角三角形.
,要求BC的长,可以运用三角函数解直角三角形.
解答:解:
(1)设A,B两处粮仓原有存粮x,y吨
根据题意得:
解得:x=270,y=180.
答:A,B两处粮仓原有存粮分别是270,180吨.
(2)A粮仓支援C粮仓的粮食是 ×270=162(吨),
×270=162(吨),
B粮仓支援C粮仓的粮食是 ×180=72(吨),
×180=72(吨),
A,B两粮仓合计共支援C粮仓粮食为162+72=234(吨).
∵234>200,
∴此次调拨能满足C粮仓需求.
(3)根据题意知:∠A=26°,AB=180千米,∠ACB=90°.
在Rt△ABC中,sin∠BAC= ,
,
∴BC=AB•sin∠BAC=180×0.44=79.2.
∵此车最多可行驶4×35=140(千米)<2×79.2,
∴小王途中须加油才能安全回到B地.
点评:求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
(2)分别求出A处和B处支援C处的粮食,将其加起来与200吨比较即可;
(3)由题意可知由已知可得△ABC中∠A=26°∠ACB=90°且AB=180Km,sin∠BAC=
 ,要求BC的长,可以运用三角函数解直角三角形.
,要求BC的长,可以运用三角函数解直角三角形.解答:解:
(1)设A,B两处粮仓原有存粮x,y吨
根据题意得:

解得:x=270,y=180.
答:A,B两处粮仓原有存粮分别是270,180吨.
(2)A粮仓支援C粮仓的粮食是
 ×270=162(吨),
×270=162(吨),B粮仓支援C粮仓的粮食是
 ×180=72(吨),
×180=72(吨),A,B两粮仓合计共支援C粮仓粮食为162+72=234(吨).
∵234>200,
∴此次调拨能满足C粮仓需求.
(3)根据题意知:∠A=26°,AB=180千米,∠ACB=90°.
在Rt△ABC中,sin∠BAC=
 ,
,∴BC=AB•sin∠BAC=180×0.44=79.2.
∵此车最多可行驶4×35=140(千米)<2×79.2,
∴小王途中须加油才能安全回到B地.
点评:求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
 C1绕点A1逆时针旋转180°,得到△A1B2C2.
C1绕点A1逆时针旋转180°,得到△A1B2C2. (2012•龙岩模拟)如图所示的几何体是由三个同样大小的正方体搭成,其左视图是( )
(2012•龙岩模拟)如图所示的几何体是由三个同样大小的正方体搭成,其左视图是( ) (2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
(2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形). 余的一半作为绿化用地.
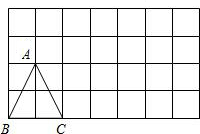
余的一半作为绿化用地. 如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中这样的格点三角形有( )个与△DEF全等.
如图,方格纸中△DEF的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则图中这样的格点三角形有( )个与△DEF全等.