题目内容
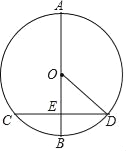
【题目】如图，在⊙O中，AB为直径，且AB⊥CD，垂足为E，CD=
，AE=5．
（1）求⊙O半径r的值；
（2）点F在直径AB上，连结CF，当∠FCD=
∠DOB时，直接写出EF的长，并在图中标出F点的具体位置．
【答案】(1)r=3;(2)见解析
【解析】分析：(1)、根据垂径定理得出计算出圆的半径；(2)、根据圆心角和圆周角的关系得出∠BCD=
∠BOD，作点B关于CD的对称点F，点F即为所求，根据EF=BE得出答案．
详解：解：(1)、∵AB为直径，AB⊥CD， ∴DE=CD=
．
在Rt△ODE中， ∵OD=r，OE=5﹣r，DE=， ∴r2=（5﹣r）2+（）2，解得r=3；
(2)、如图，连接CB．
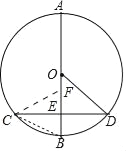
∵∠BCD=
∠BOD， 作点B关于CD的对称点F，点F即为所求．
∴EF=EB=OB﹣OE=3﹣2=1．
练习册系列答案
阅读快车系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐多重多少千克？
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.8元，则出售这20筐白菜可卖多少元？（结果保留整数）
