��Ŀ����
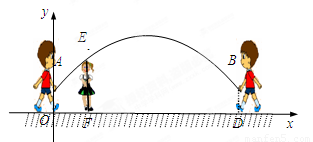
����ʱ,��˦����ߴ�ʱ����״�������ߣ�����˦���ļף�������ͬѧ�������ּ��ABΪ6��,������ľ���AO��BD��Ϊ0��9��,����Ϊ1��4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��,����˦����ߴ�ʱ�պ�ͨ������ͷ����E���Ե�OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ, ��������ߵĽ���ʽΪy=ax2��bx��0��9��
��1����������ߵĽ���ʽ ��
��2�����С��վ��OD֮��,�����O�ľ���Ϊ3��,������˦����ߴ�ʱ�պ�ͨ������ͷ��,С��������Ϊ ;
��3���������Ϊ1��4��С��վ��OD֮��,�����O�ľ���Ϊt��, ����˦����ߴ�ʱ��������ͷ��,����ͼ��,д��t��ȡֵ��Χ ��
��1�������ߵĽ���ʽ��y=��0.1x2+0.6x+0.9;��2��С����������1.8��;��3��1��t��5��
��������
�������:��1����֪�����߽���ʽ,�����еĴ���ϵ��,ѡ��������������E��1,1.4��,B��6,0.9��������뼴��;
��2��С��վ��OD֮��,�����O�ľ���Ϊ3��,��OF=3,��x=3ʱ,����ֵ;
��3��ʵ���Ͼ�����y=1.4ʱ,��Ӧ��x������ֵ,����t��ȡֵ��Χ��
�������:��1��������õ�E��1,1.4��,B��6,0.9��,����y=ax2+bx+0.9��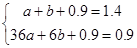 ,
,
���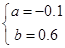 ,
,
������������ߵĽ���ʽ��y=��0.1x2+0.6x+0.9;
��2����x=3����y=��0.1x2+0.6x+0.9��
y=��0.1��32+0.6��3+0.9=1.8
������������1.8��;
��3����y=1.4ʱ,��0.1x2+0.6x+0.9=1.4,
���x1=1,x2=5,
��1��t��5��
����:���κ�����Ӧ�ã�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�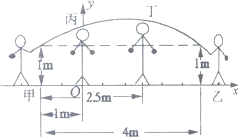 ��֪����ƽʱ����������ʱ����˦����ߴ�����״�ɽ��Ƶؿ�Ϊ�����ߣ���ͼ������˦���ļס�������ѧ���������ּ����Ϊ4m��������Ϊ1m��ѧ���������ֱ�վ�ھ����������ˮƽ����1m��2.5m����������˦����ߴ�ʱ�պ�ͨ�����ǵ�ͷ������֪ѧ����������1.5m����ѧ����������Ϊ
��֪����ƽʱ����������ʱ����˦����ߴ�����״�ɽ��Ƶؿ�Ϊ�����ߣ���ͼ������˦���ļס�������ѧ���������ּ����Ϊ4m��������Ϊ1m��ѧ���������ֱ�վ�ھ����������ˮƽ����1m��2.5m����������˦����ߴ�ʱ�պ�ͨ�����ǵ�ͷ������֪ѧ����������1.5m����ѧ����������Ϊ ��������ͼ��д��t��ȡֵ��Χ
��������ͼ��д��t��ȡֵ��Χ ����ʱ����˦����ߴ�ʱ����״�������ߣ�����˦���ļס�������ͬѧ�������ּ��ABΪ6�ף������� �ľ���AO��BD��Ϊ0.9�ף�����Ϊ1.4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��������˦����ߴ�ʱ�պ�ͨ������ͷ����E���Ե�oΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������ߵĽ���ʽΪy=ax2+bx+0.9��
����ʱ����˦����ߴ�ʱ����״�������ߣ�����˦���ļס�������ͬѧ�������ּ��ABΪ6�ף������� �ľ���AO��BD��Ϊ0.9�ף�����Ϊ1.4��С��վ�ھ��O��ˮƽ����Ϊ1�ĵ�F��������˦����ߴ�ʱ�պ�ͨ������ͷ����E���Ե�oΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ����������ߵĽ���ʽΪy=ax2+bx+0.9��