题目内容
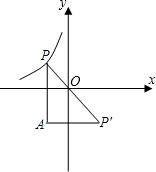 如图,设P是函数y=-
如图,设P是函数y=-| 4 |
| x |
| A、2 | B、4 |
| C、8 | D、随P的变化而变化 |
分析:设出点P的坐标,可得到P′坐标,表示出所求三角形的面积,整理即可.
解答:解:设点P的坐标为(x,y),则P′的坐标为(-x,-y),
∴PA=2y,P′A=-2x,
∴△PAP′的面积=
×2y×(-2x)=-2xy=8,
故选C.
∴PA=2y,P′A=-2x,
∴△PAP′的面积=
| 1 |
| 2 |
故选C.
点评:考查反比例函数的综合应用;得到所求三角形的两直角边长是解决本题的易错点.

练习册系列答案
相关题目
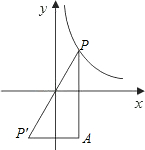 如图,设P是函数
如图,设P是函数 在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PP′A的面积为 .
在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PP′A的面积为 .
 在第二象限的图象上的任意一点,点P关于原点的对称点P′,过P作PA∥y轴,过P′作P′A∥x轴,PA与P′A交于点A,则△PAP′的面积是( )
在第二象限的图象上的任意一点,点P关于原点的对称点P′,过P作PA∥y轴,过P′作P′A∥x轴,PA与P′A交于点A,则△PAP′的面积是( )
 在第二象限的图象上的任意一点,点P关于原点的对称点P′,过P作PA∥y轴,过P′作P′A∥x轴,PA与P′A交于点A,则△PAP′的面积是( )
在第二象限的图象上的任意一点,点P关于原点的对称点P′,过P作PA∥y轴,过P′作P′A∥x轴,PA与P′A交于点A,则△PAP′的面积是( )