Question

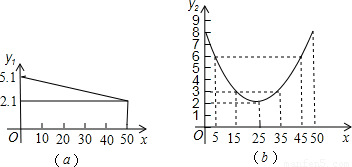
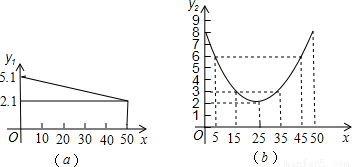
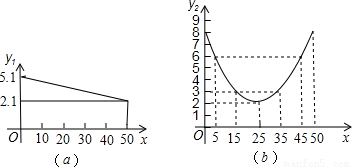
某蔬菜基地种植的某种绿色蔬菜，根据今年的市场行情，预计从5月1日起的50天内，它的市场售价y₁与上市时间x的关系可用图A的一条线段表示；它的种植成本y₂与上市时间x的关系可用图B中的抛物线的一部分来表示．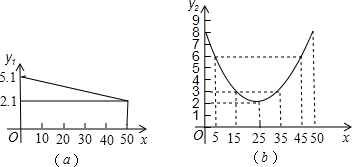

（1）求出图A中表示的市场售价y₁与上市时间x的函数关系式．
（2）求出图B中表示的种植成本y₂与上市时间x的函数关系式．
（3）假定市场售价减去种植成本为纯利润，问哪天上市的这种绿色蔬菜既不赔本也不赚钱？（市场售价和种植成本的单位：元/千克，时间单位：天）

Answer 1

分析：（1）设y=kx+b，因为函数图象过点（0，5.1），（50，2.1），求出k、b，
（2）设y₂=a（x-25）²+2．因其图象过点（15，3），求出a，
（3）列出纯利润的关系式，令纯利润为0，求出x．

解答：解：（1）设y=kx+b，
∵函数图象过点（0，5.1），（50，2.1），
∴

b=5.1 50k+b=2.1

（1分）
解得：k=-

3

50

，b=5.1，（12分）
∴y1=-

3

50

x+5.1（0≤x≤50）．（3分）

（2）又由题目已知条件可设y₂=a（x-25）²+2．因其图象过点（15，3）．（4分）
∴3=a（15-25）²+2，∴a=

1

100

，（5分）
∴y2=

1

100

x2-

1

2

x+

33

4

或y2=

1

100

(x-25)2+2（0≤x≤50）（6分）

（3）第x天上市的这种绿色蔬菜的纯利润为：y₁-y₂=

1

100

（x²-44x+315）（0≤x≤50）．
依题意：y₁-y₂=0，
即x²-44x+315=0，
∴（x-9）（x-35）=0，
解得：x₁=9，x₂=35．
所以从5月1日起的第9天或第35天出售的这种绿色蔬菜，既不赔本也不赚钱．

点评：本题主要考查二次函数的应用，利用顶点坐标式求二次函数解析式较简单，运用二次函数解决实际问题，比较简单．