题目内容
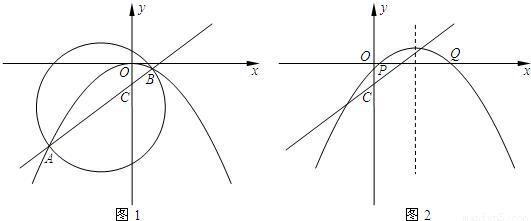
如图1,直线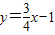 与抛物线
与抛物线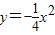 交于A、B两点(A在B的左侧),与y轴交于点C.
交于A、B两点(A在B的左侧),与y轴交于点C.(1)求线段AB的长;
(2)若以AB为直径的圆与直线x=m有公共点,求m的取值范围;
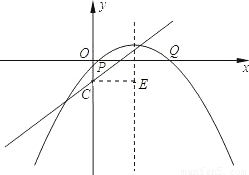
(3)如图2,把抛物线向右平移2个单位,再向上平移n个单位(n>0),抛物线与x轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时n的值;若不存在,请说明理由.
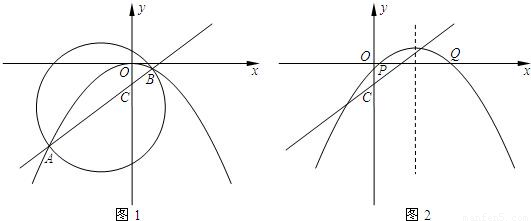
【答案】分析:(1)直线解析式与二次函数解析式组成方程组,求得点A,B的坐标,从而求得AB的长.
(2)由点A,B求得圆的圆心设为点O,由AB的长度求得圆半径而得到圆方程,代入x=m求判别式≥0即可.
(3)由抛物线平移后为: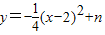 ,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,求得圆的面积和n的值.
,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,求得圆的面积和n的值.
解答:解:由题意: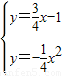 ,
,
解得:x2+3x-4=0,
即x=-4或x=1.
代入求得y=-4或- ,
,
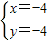 或
或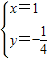 ,
,
即点A(-4,-4)B(1,- ),
),
则AB= ;
;
(2)由(1)可得A,B中点即圆的圆心点O为(- ,-
,-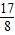 ),
),
半径为 AB=
AB=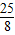 ,
,
∵以AB为直径的圆与x=m②有公共点,
∴- -
-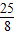 ≤m≤-
≤m≤- +
+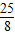 ,
,
即-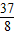 ≤m≤
≤m≤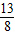 ;
;
(3)抛物线平移后为: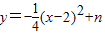 .
.
存在.
理由如下:抛物线平移后为: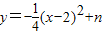 ,其对称轴是x=2.
,其对称轴是x=2.
由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为4π,n的值0.75.
点评:本题考查了二次方程的综合运用,运用直线和二次函数方程求得交点坐标,以及通过求二次方程的判别式是否≥0,来判定其是否有解.以及考查抛物线的移动问题.
(2)由点A,B求得圆的圆心设为点O,由AB的长度求得圆半径而得到圆方程,代入x=m求判别式≥0即可.
(3)由抛物线平移后为:
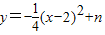 ,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,求得圆的面积和n的值.
,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,求得圆的面积和n的值.解答:解:由题意:
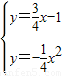 ,
,解得:x2+3x-4=0,
即x=-4或x=1.
代入求得y=-4或-
 ,
,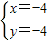 或
或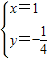 ,
,即点A(-4,-4)B(1,-
 ),
),则AB=
 ;
;(2)由(1)可得A,B中点即圆的圆心点O为(-
 ,-
,-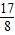 ),
),半径为
 AB=
AB=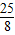 ,
,∵以AB为直径的圆与x=m②有公共点,
∴-
 -
-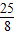 ≤m≤-
≤m≤- +
+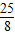 ,
,即-
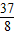 ≤m≤
≤m≤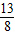 ;
;(3)抛物线平移后为:
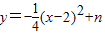 .
.
存在.
理由如下:抛物线平移后为:
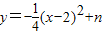 ,其对称轴是x=2.
,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为4π,n的值0.75.
点评:本题考查了二次方程的综合运用,运用直线和二次函数方程求得交点坐标,以及通过求二次方程的判别式是否≥0,来判定其是否有解.以及考查抛物线的移动问题.

练习册系列答案
相关题目
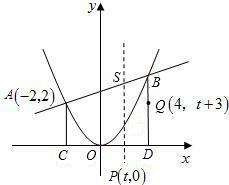 Q(4,t+3)分别为线段CD和BD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.
Q(4,t+3)分别为线段CD和BD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.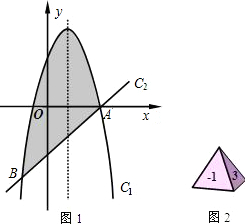 0)和点B.
0)和点B.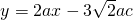 与抛物线交于E、F,与y轴交于点M,抛物线与y轴交于点N,若抛物线对称轴为直线x=2a,△MNE与△MNF面积之比为2:1,求证:△ABC为等腰直角三角形;
与抛物线交于E、F,与y轴交于点M,抛物线与y轴交于点N,若抛物线对称轴为直线x=2a,△MNE与△MNF面积之比为2:1,求证:△ABC为等腰直角三角形;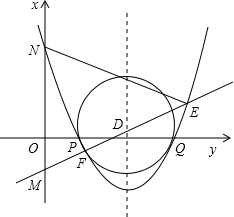
 与抛物线
与抛物线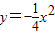 交于A、B两点(A在B的左侧),与y轴交于点C.
交于A、B两点(A在B的左侧),与y轴交于点C.