题目内容
三角形三边长分别为4、1-2a、7，则a的取值范围．
解：由三角形三边关系定理得7-4＜1-2a＜7+4，即-5＜a＜-1．
∴a的取值范围是-5＜a＜-1．
分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边；即可列不等式求第三边长的范围，从而求a的取值范围．
点评：此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
∴a的取值范围是-5＜a＜-1．
分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边；即可列不等式求第三边长的范围，从而求a的取值范围．
点评：此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
练习册系列答案
相关题目
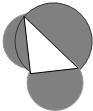如图，一直角三角形三边长分别为3，4，5，且是三个半圆的直径，求阴影部分面积（π取3.14）．
如图，一直角三角形三边长分别为6，8，10，且分别是三个半圆的直径，求阴影部面积（π取3）．