题目内容
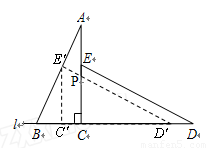
如图,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较小直角边的长为6cm,较小锐角的度数为30°.(1)将△ECD沿直线AC翻折到如图(a)的位置,ED′与AB相交于点F,请证明:AF=FD′;
(2)将△ECD沿直线l向左平移到(b)的位置,使E点落在AB上,你可以求出平移的距离,试试看;
(3)将△ECD绕点C逆时针方向旋转到图(c)的位置,使E点落在AB上,请求出旋转角的度数.

【答案】分析:(1)根据题意:由轴对称的性质容易证明:△AFE≌△D′FB;故AF=FD′;
(2)根据平移的性质可知CC′为平移的距离,先求BC′的长度,进而可得平移的距离.
(3)△ECD绕点C旋转的度数即∠ECE’的度数;易得△BCE′为等边三角形,∠ECE’=∠BAC=30度.
解答:解:(1)根据轴对称的性质可知,在△AFE与△D′FB中,
∵∠A=∠D′,AE=BD′,∠AFE=∠D′FB,
∴△AFE≌△D′FB.
∴AF=FD′.
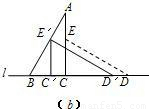 (2)根据平移的性质可知CC′为平移的距离.
(2)根据平移的性质可知CC′为平移的距离.
∵在Rt△ABC中,BC=6,∠A=30°,
∴AB=2BC=12,AC=6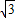 .
.
∵C′E′∥CE,
∴△BC′E′∽△BCA,
∴BC′:BC=E′C′:AC,
∴BC′=2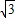 ,
,
∴CC′=6-2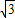 .
.
(3)根据旋转的性质可知,△BCE′为等边三角形,∠ECE′为旋转角.
∴旋转角∠ECE′为30°.
点评:本题考查平移、旋转的性质;平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.
(2)根据平移的性质可知CC′为平移的距离,先求BC′的长度,进而可得平移的距离.
(3)△ECD绕点C旋转的度数即∠ECE’的度数;易得△BCE′为等边三角形,∠ECE’=∠BAC=30度.
解答:解:(1)根据轴对称的性质可知,在△AFE与△D′FB中,
∵∠A=∠D′,AE=BD′,∠AFE=∠D′FB,
∴△AFE≌△D′FB.
∴AF=FD′.
 (2)根据平移的性质可知CC′为平移的距离.
(2)根据平移的性质可知CC′为平移的距离.∵在Rt△ABC中,BC=6,∠A=30°,
∴AB=2BC=12,AC=6
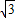 .
.∵C′E′∥CE,
∴△BC′E′∽△BCA,
∴BC′:BC=E′C′:AC,
∴BC′=2
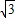 ,
,∴CC′=6-2
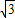 .
.(3)根据旋转的性质可知,△BCE′为等边三角形,∠ECE′为旋转角.
∴旋转角∠ECE′为30°.
点评:本题考查平移、旋转的性质;平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目

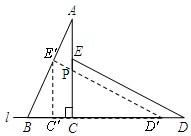 如图,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到图的位置,使E点落在AB上,即点E′,点P为AC与E′D′的交点.
如图,桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到图的位置,使E点落在AB上,即点E′,点P为AC与E′D′的交点.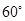 .将
.将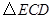 沿直线
沿直线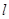 向左平移到图的位置,使E点落在AB上,即点
向左平移到图的位置,使E点落在AB上,即点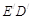 的交点.
的交点.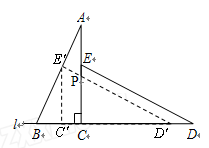
 上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为
上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为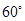 .将
.将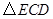 沿直线
沿直线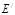 ,点P为AC与
,点P为AC与 的交点.
的交点.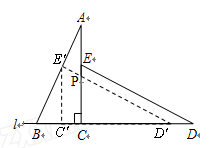
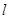 上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为
上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为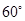 .将
.将 沿直线
沿直线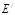 ,点P为AC与
,点P为AC与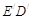 的交点.
的交点.