题目内容
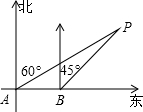
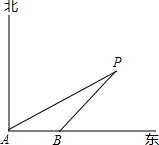 如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
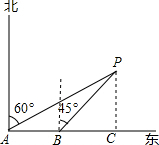 解:过点P作PC⊥AB于C点,根据题意,得
解:过点P作PC⊥AB于C点,根据题意,得AB=18×
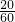 =6(海里),∠PAB=90°-60°=30°,∠PBC=90°-45°=45°,∠PCB=90°,
=6(海里),∠PAB=90°-60°=30°,∠PBC=90°-45°=45°,∠PCB=90°,∴PC=BC
在Rt△PAC中
tan30°=
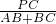 =
=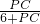
即
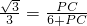 ,
,解得PC=(
 +3)海里,
+3)海里,∵
 +3>6,
+3>6,∴海轮不改变方向继续前进无触礁危险.
分析:过点P作PC⊥AB于C点,在Rt△PBD和Rt△PAC中,根据三角函数AC、BC就可以PC表示出来,在直角△PAC中,根据三角函数,就得到一个关于PC的方程,求得PC.进而判断如果海轮不改变方向继续前进有没有暗礁的危险.
点评:本题主要考查解直角三角形在实际问题中的应用,构造直角三角形是解题的前提和关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?
如图,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?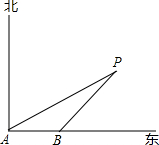 如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有暗礁的危险?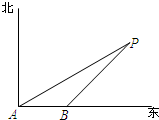 如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘渔船跟踪鱼群由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶6海里后,到达B处又测得灯塔P在它的北偏东45°方向上,如果渔船不改变方向继续前进有没有触礁的危险?
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘渔船跟踪鱼群由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶6海里后,到达B处又测得灯塔P在它的北偏东45°方向上,如果渔船不改变方向继续前进有没有触礁的危险?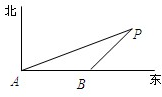 如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以24海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东30°方向上,如果海轮不改变方向继续前进有没有触礁的危险?
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以24海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东30°方向上,如果海轮不改变方向继续前进有没有触礁的危险?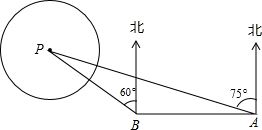 如图,海上有一灯塔P,在它周围4千米内有暗礁,一艘轮船以每小时9千米的速度由东向西行驶,行至A处测得灯塔P在它的北偏西75?,继续行驶一小时到达B处,又测得灯塔P在它的北偏西60?,试问:若客轮不改变航向,是否有触礁的危险?(供考生参考的数据:tan15°≈0.2679,cot15°≈3.732,
如图,海上有一灯塔P,在它周围4千米内有暗礁,一艘轮船以每小时9千米的速度由东向西行驶,行至A处测得灯塔P在它的北偏西75?,继续行驶一小时到达B处,又测得灯塔P在它的北偏西60?,试问:若客轮不改变航向,是否有触礁的危险?(供考生参考的数据:tan15°≈0.2679,cot15°≈3.732,