题目内容
6、两圆半径长分别是R和r(R>r),圆心距为d,若关于x的方程x2-2rx+(R-d)2=0有相等的两实数根,则两圆的位置关系是
外切或内切
.分析:一元二次方程有相等的两实数根,即△=0,从而得出R、r与d的关系式,针对两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系得出两圆位置关系.
解答:解:依题意,4r2-4(R-d)2=0,即r2-(R-d)2=0,
则:(R+r-d)(r+d-R)=0,
即R+r-d=0或r+d-R=0,
所以R+r=d或d=R-r,所以两圆的位置关系是外切或内切.
则:(R+r-d)(r+d-R)=0,
即R+r-d=0或r+d-R=0,
所以R+r=d或d=R-r,所以两圆的位置关系是外切或内切.
点评:考查一元二次方程根的判别式和圆与圆的位置关系,同时考查综合应用能力及推理能力.

练习册系列答案
相关题目
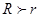 ),圆心距为d,若关于x的方程
),圆心距为d,若关于x的方程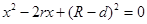 有相等的两实数根,则两圆的位置关系是_________.
有相等的两实数根,则两圆的位置关系是_________.