题目内容
【题目】如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是 .(只需写出一个即可,图中不能再添加别的“点”和“线”)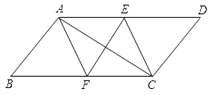
【答案】AC⊥EF
【解析】解:则添加的一个条件可以是:AC⊥EF.
证明:∵AD∥BC,
∴∠FAD=∠AFB,
∵AF是∠BAD的平分线,
∴∠BAF=FAD,
∴∠BAF=∠AFB,
∴AB=BF,
同理ED=CD,
∵AD=BC,AB=CD,
∴AE=CF,
又∵AE∥CF
∴四边形AECF是平行四边形,
∵对角线互相平分且垂直的四边形是菱形,
则添加的一个条件可以是:AC⊥EF.
故答案为:AC⊥EF.
菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.根据平行四边形的判定可得四边形AECF是平行四边形,由平行四边形的性质知,对角线互相平分,又对角线互相平分且垂直的四边形是菱形,可得:当AC⊥EF时,四边形AECF是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目