题目内容
在半径为1的⊙O中,弦AB、AC长分别为| 3 |
| 2 |
分析:首先根据题意画出图形,连接OA,作OM⊥AB,ON⊥AC,由已知条件可知,OA=1,AM=
,AN=
,然后根据勾股定理和锐角三角函数的性质,可得∠OAN=45°,∠OAM=30°,即可得∠BAC的度数.
| ||
| 2 |
| ||
| 2 |
解答: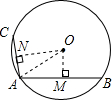 解:①如图,连接OA,作OM⊥AB,ON⊥AC,
解:①如图,连接OA,作OM⊥AB,ON⊥AC,
∵AB、AC为⊙0的弦,
∴AM=
,AN=
,
∵OA=1,
∴在Rt△ONA和Rt△OMA中,
∴∠OAN=45°,∠OAM=30°,
∴∠BAC=75°.
②若AC和AB在圆心同侧时,则∠BAC=45°-30°=15°,
故答案为:75°或15°.
 解:①如图,连接OA,作OM⊥AB,ON⊥AC,
解:①如图,连接OA,作OM⊥AB,ON⊥AC,∵AB、AC为⊙0的弦,
∴AM=
| ||
| 2 |
| ||
| 2 |
∵OA=1,
∴在Rt△ONA和Rt△OMA中,
∴∠OAN=45°,∠OAM=30°,
∴∠BAC=75°.
②若AC和AB在圆心同侧时,则∠BAC=45°-30°=15°,
故答案为:75°或15°.
点评:本题主要考查了垂径定理、勾股定理、锐角三角函数的逆定理,解题的关键在于根据题意画出图形,构建直角三角形,根据三边关系求出锐角的度数.

练习册系列答案
相关题目