题目内容
以关于x、y的方程组
的解为坐标的点(x,y)在第二象限.则符合条件的实数m的范围为( )
|
A、m>
| ||
| B、m<-2 | ||
C、-2<m<
| ||
D、-
|
分析:解出方程组的解,根据已知得x<0,y>0,再解不等式组,可求出m的取值范围.
解答:解:解方程组
得
,
∵x<0,y>0,
∴
<0,
>0,
∴m<-2.
故选B.
|
|
∵x<0,y>0,
∴
| 9m+18 |
| 9m2+2 |
| 3-27m |
| 9m2+2 |
∴m<-2.
故选B.
点评:本题是已知方程组的解,求方程组中另一字母参数的取值范围问题.可以先解出方程组,转化为不等式组问题.求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
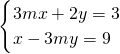 的解为坐标的点(x,y)在第二象限.则符合条件的实数m的范围为
的解为坐标的点(x,y)在第二象限.则符合条件的实数m的范围为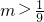
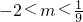
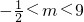
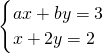 只有正数解的概率.
只有正数解的概率.