题目内容
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值.
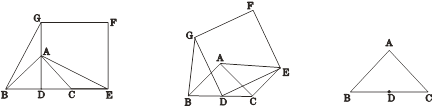
图1 图2 备用图
【答案】(1)证明见解析;(2)成立;(3)270°,![]()
【解析】试题分析(1)在Rt△BDG与Rt△EDA;根据边角边定理易得Rt△BDG≌Rt△EDA;故BG=AE;
(2)连接AD,根据直角三角形与正方形的性质可得Rt△BDG≌Rt△EDA;进而可得BG=AE;
(3)根据(2)的结论,求BG的最大值,分析可得此时F的位置,由勾股定理可得答案.
试题解析:(1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°,AD=DC=DB,
∵四边形DEFG是正方形,
∴DE=DG,
∴△ADE≌△BDG(SAS),
∴BG=AE;
(2)成立;
理由如下:如图2,连接AD,
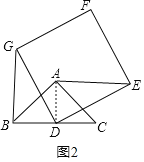
由(1)知AD=BD,AD⊥BC.
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°.
∴∠ADG+∠ADE=90°
∴∠BDG=∠ADE.
在△BDG和△ADE中,
∵BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE(SAS)
∴AE=BG;
(3)α=270°;
正方形DEFG如图3所示
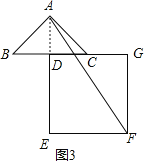
由(2)知BG=AE
∴当BG取得最大值时,AE取得最大值.
∵BC=DE=4,
∴EF=4,
∴BG=2+4=6
∴AE=6
在Rt△AEF中,由勾股定理,得
AF=![]() .
.