题目内容
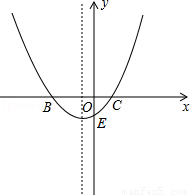
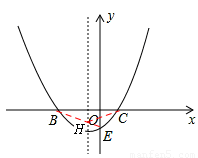
如图,已知抛物线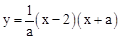 (a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线过点M(﹣2,﹣2),求实数a的值;
(2)在(1)的条件下,解答下列问题;
①求出△BCE的面积;
②在抛物线的对称轴上找一点H,使CH+EH的值最小,直接写出点H的坐标.
【答案】
(1)a=4
(2)①6
②(﹣1,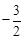 )
)
【解析】
试题分析:(1)将M坐标代入抛物线解析式求出a的值即可;
将M(﹣2,﹣2)代入抛物线解析式得: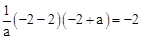 ,解得:a=4。
,解得:a=4。
(2)①求出的a代入确定出抛物线解析式,令y=0求出x的值,确定出B与C坐标,令x=0求出y的值,确定出E坐标,进而得出BC与OE的长,即可求出三角形BCE的面积。
①由(1)抛物线解析式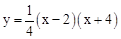 ,
,
当y=0时,得: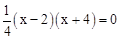 ,解得:x1=2,x2=﹣4。
,解得:x1=2,x2=﹣4。
∵点B在点C的左侧,∴B(﹣4,0),C(2,0)。
当x=0时,得:y=﹣2,∴E(0,﹣2)。
∴S△BCE=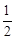 ×6×2=6。
×6×2=6。
②∵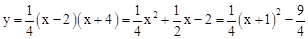 ,∴抛物线对称轴为直线x=﹣1。
,∴抛物线对称轴为直线x=﹣1。
根据C与B关于抛物线对称轴直线x=﹣1对称,连接BE,与对称轴交于点H,即为所求。
设直线BE解析式为y=kx+b,
将B(﹣4,0)与E(0,﹣2)代入得:
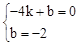 ,解得:
,解得: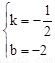 。
。
∴直线BE解析式为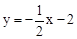 。
。
将x=﹣1代入得: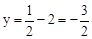 ,∴H(﹣1,
,∴H(﹣1,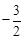 )。
)。

练习册系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;