题目内容
等腰三角形一边上的高等于这边的一半,则它的顶角度数是________.
30°或90°或120°或150°
解:如图,分四种情况:
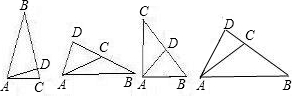
1、AB=BC,AD⊥BC,AD在三角形的内部,由题意知,AD=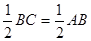
∵sin∠B=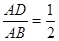
∴∠B=30°;
2、AC=BC,AD⊥BC,AD在三角形的外部,由题意知,AD=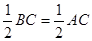
∵sin∠ACD=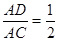
∴∠ACD=30°,
∴∠ACB=180°-30°=150°;
3、AB=AC,AD⊥BC,BC边为等腰三角形的底边,
由等腰三角形的底边上的高、底边上中线、顶角的平分线互相重合知,点D为BC的中点,
由题意知,AD=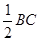 =CD=BD,
=CD=BD,
∴△ABD,△ADC均为等腰直角三角形,
∴∠BAD=∠CAD=45°,
∴∠BAC=90°.
4、AC=BC,AD⊥BC,AD在三角形的外部,由题意知,AD=
∵sin∠B=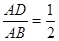
∴∠B=30°,
∴∠ACB=180°-30°-30°=120°;
故填30°、90°、120°或150°.

1、AB=BC,AD⊥BC,AD在三角形的内部,由题意知,AD=
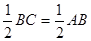
∵sin∠B=
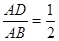
∴∠B=30°;
2、AC=BC,AD⊥BC,AD在三角形的外部,由题意知,AD=
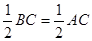
∵sin∠ACD=
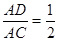
∴∠ACD=30°,
∴∠ACB=180°-30°=150°;
3、AB=AC,AD⊥BC,BC边为等腰三角形的底边,
由等腰三角形的底边上的高、底边上中线、顶角的平分线互相重合知,点D为BC的中点,
由题意知,AD=
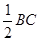 =CD=BD,
=CD=BD,∴△ABD,△ADC均为等腰直角三角形,
∴∠BAD=∠CAD=45°,
∴∠BAC=90°.
4、AC=BC,AD⊥BC,AD在三角形的外部,由题意知,AD=

∵sin∠B=
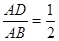
∴∠B=30°,
∴∠ACB=180°-30°-30°=120°;
故填30°、90°、120°或150°.

练习册系列答案
相关题目
 北偏西
北偏西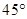 并距该岛
并距该岛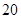 海里的
海里的 处待命.位于该岛正西方向
处待命.位于该岛正西方向 处的某渔船遭到袭扰,船长发现在其北偏东
处的某渔船遭到袭扰,船长发现在其北偏东 的方向有我海监84、75船编队(如图所示),便发出紧急求救信号.我海监84、75船编队接到信号后,立即沿
的方向有我海监84、75船编队(如图所示),便发出紧急求救信号.我海监84、75船编队接到信号后,立即沿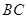 航线以每小时60海里的速度前去实施现场保护.问我海监84、75船编队需多少分钟可以到达该渔船所在的位置
航线以每小时60海里的速度前去实施现场保护.问我海监84、75船编队需多少分钟可以到达该渔船所在的位置 )
)
 ;
;
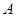 ,用测角仪测出看塔顶
,用测角仪测出看塔顶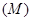 的仰角
的仰角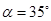 ,在
,在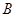 ,测出看塔顶
,测出看塔顶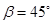 ,然后用皮尺量出
,然后用皮尺量出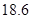 m,自身的高度为
m,自身的高度为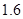 m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(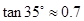 ,结果保留整数).
,结果保留整数).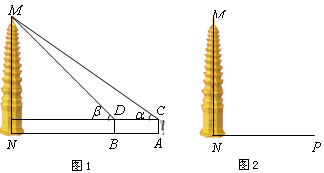
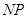 的长为
的长为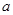 m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,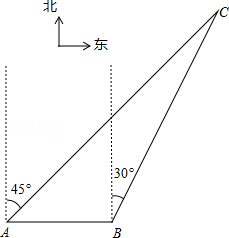
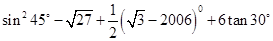
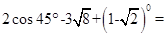 .
.