题目内容
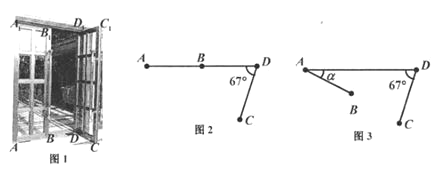
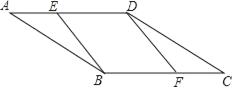
【题目】如图是一个儿童游乐场所,由于周末小朋友较多,老板计划将场地扩建,扩建前平面图为△ABC,BC=10米,∠ABC=∠ACB=36°,扩建后顶点D在BA的延长线上,且∠BDC=90°,求扩建后AB边增加部分AD的长.(结果精确到0.1米.参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)

【答案】1.9米.
【解析】
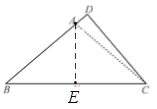
试题过A作AE⊥BC于点E,在直角三角形ABE中,由BE与cosB的值,利用锐角三角函数定义求出AB的长,在直角三角形BCD中,由∠ABC度数,以及BC的长,利用锐角三角函数定义求出BD的长,从而即可得.
试题解析:过A作AE⊥BC于点E,∵AB=AC,∴BE=EC=![]() BC=5.
BC=5.
在Rt△ABE中,cosB=![]() ,∴AB=
,∴AB=![]() ≈6.17.
≈6.17.
在Rt△BDC中,cosB=![]() ,∴BD=10×cos36°≈8.1,∴AD=BD-AB=1.93≈1.9.
,∴BD=10×cos36°≈8.1,∴AD=BD-AB=1.93≈1.9.
故扩建后AB边增加部分AD的长为1.9米.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目