题目内容
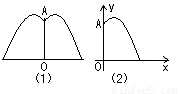
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线的形状如图(1)和(2)所示,建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=-x2+2x+| 5 | 4 |
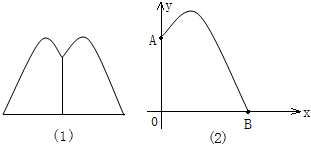 (1)柱子OA的高度为多少米?
(1)柱子OA的高度为多少米?(2)喷出的水流距水平面的最大高度是多少?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
分析:在已知抛物线解析式的情况下,利用其性质,求顶点(最大高度),与x轴,y轴的交点,解答题目的问题.
解答:解:(1)当x=0时,y=
,
故OA的高度为1.25米;
(2)∵y=-x2+2x+
=-(x-1)2+2.25,
∴顶点是(1,2.25),
故喷出的水流距水面的最大高度是2.25米;
(3)解方程-x2+2x+
=0,
得x1=-
,x2=
,
∴B点坐标为(
,0),
∴OB=
.
故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
| 5 |
| 4 |
故OA的高度为1.25米;
(2)∵y=-x2+2x+
| 5 |
| 4 |
∴顶点是(1,2.25),
故喷出的水流距水面的最大高度是2.25米;
(3)解方程-x2+2x+
| 5 |
| 4 |
得x1=-
| 1 |
| 2 |
| 5 |
| 2 |
∴B点坐标为(
| 5 |
| 2 |
∴OB=
| 5 |
| 2 |
故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
点评:本题是抛物线解析式的实际应用,要求掌握抛物线顶点,与x轴交点,y轴交点的实际意义.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,请回答下列问题.
,请回答下列问题.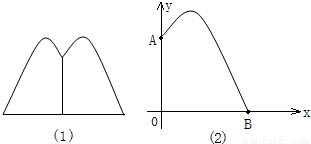
 ,请回答下列问题.
,请回答下列问题.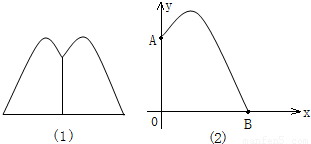
 ,请回答下列问题.
,请回答下列问题.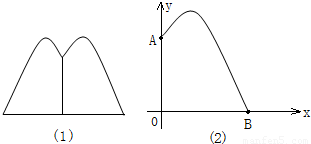
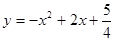 .请回答下列问题:
.请回答下列问题: