题目内容
(2008•太原)如图,在平面直角坐标系xOy中,直线y=x+1与y=- x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.(1)求点A,B,C的坐标;
(2)当△CBD为等腰三角形时,求点D的坐标;
(3)在直线AB上是否存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形?如果存在,直接写出
 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】分析:(1)令y=0,代入直线解析式求出B,C点坐标.联立方程组后可求出点A的坐标.
(2)当△CBD为等腰三角形时,分三种情况讨论(BD1=D1C;BC=BD2;CD3=BC,或CD4=BC),依靠辅助线的帮助求出点D的坐标.
(3)本题也要借助辅助线的帮助.分为三种情况讨论(当四边形AE1OD1为平行四边形;当四边形AD2E1O为平行四边形时;当四边形AOD1E2为平行四边形时).
解答:解:(1)在y=x+1中,当y=0时,x+1=0,∴x=-1,点B的坐标为(-1,0). (1')
在y=- x+3中,当y=0时,-
x+3中,当y=0时,- x+3=0,∴x=4,点C的坐标为(4,0). (2分)
x+3=0,∴x=4,点C的坐标为(4,0). (2分)
由题意,得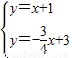 解得
解得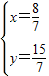
∴点A的坐标为( ,
,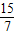 ).(3分)
).(3分)
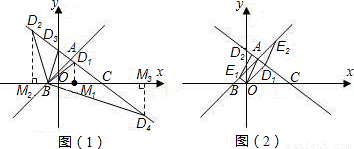
(2)当△CBD为等腰三角形时,有以下三种情况,如图(1).设动点D的坐标为(x,y).
由(1),得B(-1,0),C(4,0),∴BC=5.
①当BD1=D1C时,过点D1作D1M1⊥x轴,垂足为点M1,则BM1=M1C= BC.
BC.
∴BM1= ,OM1=
,OM1= -1=
-1= ,x=
,x= .
.
∴y=-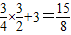 ,点D1的坐标为
,点D1的坐标为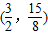 .(4分)
.(4分)
②当BC=BD2时,过点D2作D2M2⊥x轴,垂足为点M2,则D2M22+M2B2=D2B2,
∵M2B=-x-1,D2M2=- x+3,D2B=5,
x+3,D2B=5,
∴(-x-1)2+(- x+3)2=52.
x+3)2=52.
解得x1=-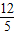 ,x2=4(舍去).此时,
,x2=4(舍去).此时,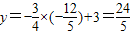 .
.
∴点D2的坐标为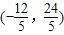 . (6分)
. (6分)
③当CD3=BC,或CD4=BC时,同理可得D3(0,3),D4(8,-3).(9分)
由此可得点D的坐标分别为D1( ,
,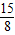 ),D2(-
),D2(-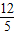 ,
,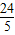 ),D3(0,3),D4(8,-3).
),D3(0,3),D4(8,-3).
评分说明:符合条件的点有4个,正确求出1个点的坐标得(1分),2个点的坐标得(3分),3个点的坐标得(5分),4个点的坐标得满分;与所求点的顺序无关.
(3)存在.以点E,D,O,A为顶点的四边形是平行四边形有以下三种情形,如图(2).
①当四边形AE1OD1为平行四边形时,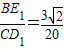 . (10分)
. (10分)
②当四边形AD2E1O为平行四边形时,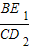 =
=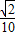 .(11分)
.(11分)
③当四边形AOD1E2为平行四边形时,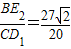 .(12分)
.(12分)
点评:本题考查的是二元一次方程组的应用,平行四边形的判定以及线段比的有关知识,难度中上.
(2)当△CBD为等腰三角形时,分三种情况讨论(BD1=D1C;BC=BD2;CD3=BC,或CD4=BC),依靠辅助线的帮助求出点D的坐标.
(3)本题也要借助辅助线的帮助.分为三种情况讨论(当四边形AE1OD1为平行四边形;当四边形AD2E1O为平行四边形时;当四边形AOD1E2为平行四边形时).
解答:解:(1)在y=x+1中,当y=0时,x+1=0,∴x=-1,点B的坐标为(-1,0). (1')
在y=-
 x+3中,当y=0时,-
x+3中,当y=0时,- x+3=0,∴x=4,点C的坐标为(4,0). (2分)
x+3=0,∴x=4,点C的坐标为(4,0). (2分)由题意,得
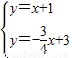 解得
解得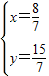
∴点A的坐标为(
 ,
,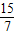 ).(3分)
).(3分)
(2)当△CBD为等腰三角形时,有以下三种情况,如图(1).设动点D的坐标为(x,y).
由(1),得B(-1,0),C(4,0),∴BC=5.
①当BD1=D1C时,过点D1作D1M1⊥x轴,垂足为点M1,则BM1=M1C=
 BC.
BC.∴BM1=
 ,OM1=
,OM1= -1=
-1= ,x=
,x= .
.∴y=-
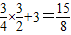 ,点D1的坐标为
,点D1的坐标为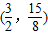 .(4分)
.(4分)②当BC=BD2时,过点D2作D2M2⊥x轴,垂足为点M2,则D2M22+M2B2=D2B2,
∵M2B=-x-1,D2M2=-
 x+3,D2B=5,
x+3,D2B=5,∴(-x-1)2+(-
 x+3)2=52.
x+3)2=52.解得x1=-
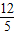 ,x2=4(舍去).此时,
,x2=4(舍去).此时,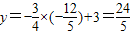 .
.∴点D2的坐标为
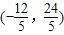 . (6分)
. (6分)③当CD3=BC,或CD4=BC时,同理可得D3(0,3),D4(8,-3).(9分)
由此可得点D的坐标分别为D1(
 ,
,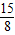 ),D2(-
),D2(-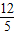 ,
,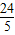 ),D3(0,3),D4(8,-3).
),D3(0,3),D4(8,-3).评分说明:符合条件的点有4个,正确求出1个点的坐标得(1分),2个点的坐标得(3分),3个点的坐标得(5分),4个点的坐标得满分;与所求点的顺序无关.
(3)存在.以点E,D,O,A为顶点的四边形是平行四边形有以下三种情形,如图(2).
①当四边形AE1OD1为平行四边形时,
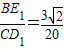 . (10分)
. (10分)②当四边形AD2E1O为平行四边形时,
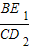 =
=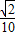 .(11分)
.(11分)③当四边形AOD1E2为平行四边形时,
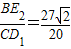 .(12分)
.(12分)点评:本题考查的是二元一次方程组的应用,平行四边形的判定以及线段比的有关知识,难度中上.

练习册系列答案
相关题目
 x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点. 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
 x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点. 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

