题目内容
 (2012•潍坊)如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(2012•潍坊)如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
分析:(1)根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE∥CF;然后由全等三角形的判定定理ASA推知△ADE≌△CBF;最后根据全等三角形的对应边相等知AE=CF,所以对边平行且相等的四边形是平行四边形;
(2)如图,连接AC交BF于点0.由菱形的判定定理推知?ABCD是菱形,根据菱形的邻边相等知AB=BC;然后结合已知条件“M是BC的中点,AM丄BC”证得△ADE≌△CBF(ASA),所以AE=CF(全等三角形的对应边相等),从而证得△ABC是正三角形;最后在Rt△BCF中,利用锐角三角函数的定义求得CF:BC=tan∠CBF=
,利用等量代换知(AE=CF,AB=BC)AB:AE=
.
(2)如图,连接AC交BF于点0.由菱形的判定定理推知?ABCD是菱形,根据菱形的邻边相等知AB=BC;然后结合已知条件“M是BC的中点,AM丄BC”证得△ADE≌△CBF(ASA),所以AE=CF(全等三角形的对应边相等),从而证得△ABC是正三角形;最后在Rt△BCF中,利用锐角三角函数的定义求得CF:BC=tan∠CBF=
| ||
| 3 |
| 3 |
解答:(1)证明∵四边形ABCD是平行四边形(已知),
∴BC∥AD(平行四边形的对边相互平行);
又∵AM丄BC(已知),
∴AM⊥AD;
∵CN丄AD(已知),
∴AM∥CN,
∴AE∥CF;
又由平行得∠ADE=∠CBD,又AD=BC(平行四边形的对边相等),
∵在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=CF(全等三角形的对应边相等),
∴四边形AECF为平行四边形(对边平行且相等的四边形是平行四边形);
(2)如图,连接AC交BF于点0, 当AECF为菱形时,
当AECF为菱形时,
则AC与EF互相垂直平分,
∵BO=OD(平行四边形的对角线相互平分),
∴AC与BD互相垂直平分,
∴?ABCD是菱形(对角线相互垂直平分的平行四边形是菱形),
∴AB=BC(菱形的邻边相等);
∵M是BC的中点,AM丄BC(已知),
∴AB=AC(等腰三角形的性质),
∴△ABC为等边三角形,
∴∠ABC=60°,∠CBD=30°;
在Rt△BCF中,CF:BC=tan∠CBF=
,
又∵AE=CF,AB=BC,
∴AB:AE=
.
∴BC∥AD(平行四边形的对边相互平行);
又∵AM丄BC(已知),
∴AM⊥AD;
∵CN丄AD(已知),
∴AM∥CN,
∴AE∥CF;
又由平行得∠ADE=∠CBD,又AD=BC(平行四边形的对边相等),
∵在△ADE和△CBF中,
|
∴△ADE≌△CBF(ASA),
∴AE=CF(全等三角形的对应边相等),
∴四边形AECF为平行四边形(对边平行且相等的四边形是平行四边形);
(2)如图,连接AC交BF于点0,
 当AECF为菱形时,
当AECF为菱形时,则AC与EF互相垂直平分,
∵BO=OD(平行四边形的对角线相互平分),
∴AC与BD互相垂直平分,
∴?ABCD是菱形(对角线相互垂直平分的平行四边形是菱形),
∴AB=BC(菱形的邻边相等);
∵M是BC的中点,AM丄BC(已知),
∴AB=AC(等腰三角形的性质),
∴△ABC为等边三角形,
∴∠ABC=60°,∠CBD=30°;
在Rt△BCF中,CF:BC=tan∠CBF=
| ||
| 3 |
又∵AE=CF,AB=BC,
∴AB:AE=
| 3 |
点评:本题综合考查了解直角三角形、全等三角形的判定与性质、菱形的判定与性质以及等边三角形的判定与性质等知识点.证明(2)题时,证得?ABCD是菱形是解题的难点.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
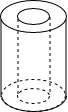 (2012•潍坊)如图空心圆柱体的主视图的画法正确的是( )
(2012•潍坊)如图空心圆柱体的主视图的画法正确的是( )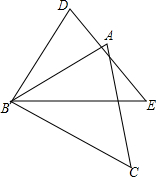 (2012•潍坊)如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件
(2012•潍坊)如图所示,AB=DB,∠ABD=∠CBE,请你添加一个适当的条件 (2012•潍坊)如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )
(2012•潍坊)如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )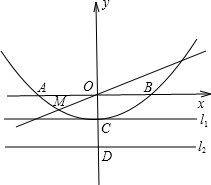 (2012•潍坊)如图,已知抛物线与坐标轴分别交于A(-2,0),B(2,0),C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)作平行于x轴的直线l1、l2.
(2012•潍坊)如图,已知抛物线与坐标轴分别交于A(-2,0),B(2,0),C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)作平行于x轴的直线l1、l2.