题目内容
已知点P的坐标是(3,3),O为原点,将线段OP绕着原点O旋转45°得到线段OQ,则点Q的坐标是 _________ .
(3 ,0)或(0,3
,0)或(0,3 ).
).
 ,0)或(0,3
,0)或(0,3 ).
).试题分析:根据P点坐标得到OP为第一象限的角平分线,利用勾股定理计算出OP=3
 ,然后分类讨论:当线段OP绕着原点O顺时针旋转45°得到线段OQ,则OQ=OP=3
,然后分类讨论:当线段OP绕着原点O顺时针旋转45°得到线段OQ,则OQ=OP=3 ,线段OQ在x轴的正半轴上;当线段OP绕着原点O逆时针旋转45°得到线段OQ,则OQ=OP=3
,线段OQ在x轴的正半轴上;当线段OP绕着原点O逆时针旋转45°得到线段OQ,则OQ=OP=3 ,线段OQ在y轴的正半轴上,再分别根据坐标轴上点的坐标特征写出Q点坐标.
,线段OQ在y轴的正半轴上,再分别根据坐标轴上点的坐标特征写出Q点坐标.试题解析:∵点P的坐标是(3,3),
∴OP为第一象限的角平分线,OP=3
 ,
,当线段OP绕着原点O顺时针旋转45°得到线段OQ,则OQ=OP=3
 ,线段OQ在x轴的正半轴上,所以Q点的坐标为(3
,线段OQ在x轴的正半轴上,所以Q点的坐标为(3 ,0);
,0);当线段OP绕着原点O逆时针旋转45°得到线段OQ,则OQ=OP=3
 ,线段OQ在y轴的正半轴上,所以Q点的坐标为(0,3
,线段OQ在y轴的正半轴上,所以Q点的坐标为(0,3 ),
),∴Q点的坐标为(3
 ,0)或(0,3
,0)或(0,3 ).
).考点: 坐标与图形变化-旋转.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 ,若点C在
,若点C在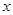 轴上,且OC=AC,求点C的坐标.
轴上,且OC=AC,求点C的坐标.
 ,
, ,∠
,∠ ,∠
,∠ ,求
,求 、
、 两点的坐标.
两点的坐标.

 关于原点对称的点的坐标是 ( ).
关于原点对称的点的坐标是 ( ).