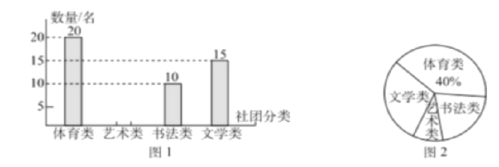
题目内容
【题目】如图,矩形纸片ABCD中,AB=4,点E在边CD上移动连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′CE,点B、C的对应点分别为点B′、C′
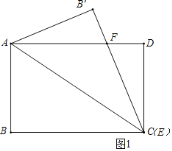
(1)当点E与点C重合时,设B′C′与AD的交点为F,若AD=4DF,则AD=______
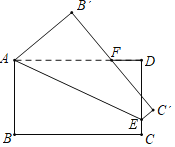
(2)若AD=6,B′C′的中点记为P,则DP的取值范围是______
【答案】4![]() 1≤DP≤5.
1≤DP≤5.
【解析】
(1)如图1,当点E与点C重合时,易知△AB'C≌△DCA,得到AF=CF,设DF=x,则AD=4x,得AF=CF=AD=DF=3x,Rt△CDF中利用勾股定理解出x,然后得到AD=4x即可 (2)如图2,点P的轨迹是以A为圆心,AP的长为半径的圆上的一段弧,当点E与点D重合时DP的值最大,易得B'P=C'P![]() 6=3,B'A=C'D=4,则AP=DP=5;当点P在AD上时,即在点P'处时,DP的值最小此时,AP=AP'=5,得DP'=AD﹣AP'=6﹣5=1,所以DP的最小值为1,
6=3,B'A=C'D=4,则AP=DP=5;当点P在AD上时,即在点P'处时,DP的值最小此时,AP=AP'=5,得DP'=AD﹣AP'=6﹣5=1,所以DP的最小值为1,
解:∵四边形ABCD为矩形,
∴AB=CD=4,AD∥BC,
∴∠DAC=∠ACB,
如图1,当点E与点C重合时,
由翻折知,△AB'C≌△DCA,
∴∠ACB'=∠ACB,
∴∠DAC=∠ACB',
∴AF=CF,
设DF=x,则AD=4x,
∴AF=CF=AD=DF=3x,
在Rt△CDF中,CF2=DF2+CD2,
∴(3x)2=x2+42,
解得,x1![]() (舍去),x2
(舍去),x2![]() ,
,
∴AD=4x=4![]() ,
,
故答案为:4![]() ;
;
(2)如图2,点P的轨迹是以A为圆心,AP的长为半径的圆上的一段弧,当点E与点D重合时DP的值最大,
∵点P是B'C'的中点,
∴B'P=C'P![]() 6=3,B'A=C'D=4,
6=3,B'A=C'D=4,
∴AP=DP![]() 5,
5,
∴DP的最大值为5,
由图可看出,当点P在AD上时,即在点P'处时,DP的值最小,
此时,AP=AP'=5,
∴DP'=AD﹣AP'=6﹣5=1,
∴DP的最小值为1,
故答案为:1≤DP≤5.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案