题目内容
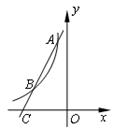
如图,⊿ACO的顶点A,C分别是双曲线 与直线
与直线 在第二象限、第四象限的交点,AB⊥
在第二象限、第四象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=

(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)根据图象写出使 的自变量x的取值范围.
的自变量x的取值范围.
 与直线
与直线 在第二象限、第四象限的交点,AB⊥
在第二象限、第四象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=

(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)根据图象写出使
 的自变量x的取值范围.
的自变量x的取值范围.(1)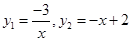 ;(2)A(-1,3),C(3,-1);(3)
;(2)A(-1,3),C(3,-1);(3)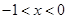 或
或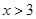
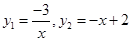 ;(2)A(-1,3),C(3,-1);(3)
;(2)A(-1,3),C(3,-1);(3)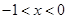 或
或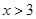
试题分析:(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)把两函数的解析式组成方程组,求出x、y的值,即可得出A、C两点的坐标;
(3)直接根据一次函数与反比例函数的交点坐标求出反比例函数的值大于一次函数的值x的取值范围即可.
(1)∵反比例函数
 的图象在二、四象限,
的图象在二、四象限,∴
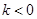
∵
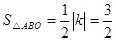
∴
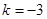
∴双曲线
 的解析式为
的解析式为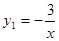
直线
 的解析式为
的解析式为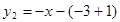 ,即
,即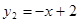 ;
;(2)∵把一次函数与反比例函数的解析式组成方程组得:
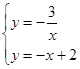 ,解得
,解得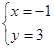 或
或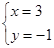
∴A(-1,3),C(3,-1);
(23)∵A(-1,3),C(3,-1),
∴当
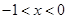 或
或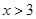 时,
时, .
.点评:解答本题的关键是熟练掌握待定系数法求一次函数及反比例函数的解析式,能根据△ABO的面积求出k的值.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 与直线
与直线 在第二象限内的交点,AB⊥
在第二象限内的交点,AB⊥ 轴于点B,且
轴于点B,且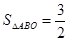 .
.
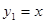 (x≥0),
(x≥0),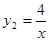 (x>0)的图象如图所示,则下列结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,
(x>0)的图象如图所示,则下列结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,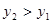 ;③当x=1时,BC=3;④当x逐渐增大时,
;③当x=1时,BC=3;④当x逐渐增大时,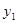 随x的增大而增大,
随x的增大而增大,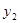 随着x的增大而减小,其中正确的结论序号是______。
随着x的增大而减小,其中正确的结论序号是______。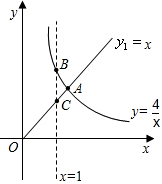
 的图象上,则y1、y2、y3的大小关系是 ___
的图象上,则y1、y2、y3的大小关系是 ___ 在同一直角坐标系中的图象大致如图,则下列结论正确的是( )
在同一直角坐标系中的图象大致如图,则下列结论正确的是( )
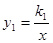 的图象与正比例函数
的图象与正比例函数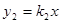 的图象交于点(2,1),则使
的图象交于点(2,1),则使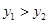 的
的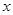 的取值范围是( )
的取值范围是( )


 或
或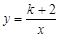 的图像位于第二、四象限,则k的值可以是 (写出满足条件的一个k的值即可)。
的图像位于第二、四象限,则k的值可以是 (写出满足条件的一个k的值即可)。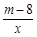 (m为常数)的图象经过点A(-1,6),过A点的直线交函数y=
(m为常数)的图象经过点A(-1,6),过A点的直线交函数y=