Question

【题目】如图，在平面直角坐标系中，点的坐标为，点的坐标为，抛物线经过、、三点，连接、、，线段交轴于点，已知实数、分别是方程的两根.

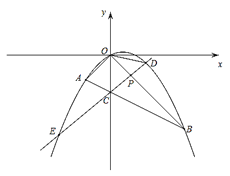
（1）求抛物线的解析式；

（2）若点为线段上的一个动点（不与点、重合），直线与抛物线交于、两点（点在轴右侧），连接、.

①求面积的最大值，并写出此时点的坐标；②当为等腰三角形时，请直接写出点的坐标.

Answer 1

【答案】（1）抛物线的解析式为：；（2）①△OBD面积最大值为，此时点D（）；②点P（）或（）或（）

【解析】

（1）解方程即可求得A和B的坐标，代入即可求得抛物线的解析式；

（2）①过D作DG⊥x轴于G，交OB于点Q，过点B作BH⊥x轴于H，用d表示D点和Q点的坐标，根据，可得S和d的关系式，进而可得的最大值以及此时点D的坐标；②求出直线AB的解析式，即可得OC的长度，设点P（p,-p）对△OPC为等腰三角形的情况分类讨论：（1）OP=OC；（2）OP=PC，；（3）OC=PC，分别根据两点间距离公式以及线段垂直平分线的性质求出p的值即可求得点P的坐标.

解：（1）∵

∴

又m<n

∴m=-1，n=3

又∵抛物线过点O（0,0）

所以将A（-1，-1），B（3，-3）代入抛物线解析式中，

可得

解得

∴抛物线的解析式为：.

（2）①如下图所示，过D作DG⊥x轴于G，交OB于点Q，过点B作BH⊥x轴于H，

设点D（d，），

易得直线OB的解析式为：y=-x

∴Q（d,-d）

∴

=

=

=

=

=

∴当时，取最大值，最大值为，此时D（）

故△OBD面积最大值为，此时点D（）.

②设直线AB的解析式为：y=kx+b，将点A（-1，-1），B（3，-3）代入得：

，解得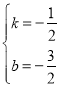

∴直线AB的解析式为：

令x=0得：y=

∴OC=

同理可知直线OB的解析式为：y=-x

∴设点P（p,-p）且p>0

根据两点间距离公式对△OPC为等腰三角形的情况分类讨论：

（1）OP=OC，∴OP=

∴p=（舍去）或p=

∴点P（）

（2）OP=PC，∴P在线段OC中垂线上

∴P的纵坐标为

又点P在OB上

∴P（）

（3）OC=PC，∴PC=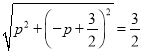

解得：p=0（舍去）或p=

∴点P（）

综上所述：点P（）或（）或（）.