题目内容
 如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(1)求抛物线的解析式;
(2)若点D为抛物线上的一点,点E为对称轴上的一点,且以点A、O、D、E为
顶点的四边形为平行四边形,请直接写出点D的坐标;
(3)若点P是抛物线第一象限上的一个动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
 解:(1)∵抛物线的顶点为C(-1,-1),
解:(1)∵抛物线的顶点为C(-1,-1),∴设抛物线的解析式为:y=a(x+1)2-1,
∵抛物线经过(0,0),
∴将x=0,y=0代入抛物线解析式得:0=a-1,
解得:a=1,
∴y=(x+1)2-1=x2+2x,
令y=0时,x2+2x=0,
解得x1=0,x2=-2,
∴A(-2,0);
(2)如图所示,分三种情况考虑:
当D1在第一象限时,若四边形AOD1E1为平行四边形,
∴AO=E1D1=2,
∵抛物线对称轴为直线x=-1,
∴D1横坐标为1,
将x=1代入抛物线y=x2+2x=1+2=3,即D1(1,3);
当D2在第二象限时,同理D2(-3,3);
当D3在第三象限时,若四边形AE2OD3为平行四边形,此时D3与C重合,即D3(-1,-1);
(3)存在,
∵点B在抛物线上,
∴当x=-3时,y=9-6=3,
∴B(-3,3),
根据勾股定理得:BO2=9+9=18;CO2=1+1=2;BC2=16+4=20,
∴BO2+CO2=18+2=20,
∴BO2+CO2=BC2,∴△BOC为直角三角形,
假设存在点P,使得以P、M、A为顶点的三角形与△BOC相似,
设P(m,n),由题意得m>0,n>0,且n=m2+2m,
①若△AMP∽△BOC,则
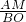 =
=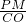 ,即
,即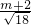 =
=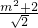 ,
,整理得:m+2=3(m2+2m)=0,即3m2+5m-2=0,
解得:m1=
 ,m2=-2(舍去),
,m2=-2(舍去),m1=
 时,n=
时,n= +
+ =
= ,
,∴P(
 ,
, );
); ②若△AMP∽△COB,则
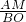 =
=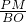 ,即
,即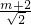 =
=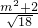 ,
,整理得:m2-m-6=0,
解得 m1=3,m2=-2(舍去),
当m=3时,n=9+6=15,
∴P(3,15),
综上所述,符合条件的点P有两个,分别是P1(
 ,
, ),P2(3,15).
),P2(3,15).分析:(1)根据顶点坐标设出抛物线的顶点式解析式,将原点坐标代入求出a的值,即可确定出抛物线解析式;
(2)分三种情况考虑,D在第一象限,第二象限以及第三象限,利用平行四边形的性质及坐标与图形性质求出D坐标即可;
(3)根据题意画出图形,根据B横坐标为-3,代入抛物线解析式求出纵坐标,确定出B坐标,进而求出BC,BO,OC的长,利用勾股定理的逆定理得到三角形BOC为直角三角形,若P、M、A为顶点的三角形与△BOC相似,设P(m,n),由题意得m>0,n>0,且n=m2+2m,根据相似得比例,列出关于m的方程,求出方程的解得到m的值,进而求出n的值,即可确定出P的坐标.
点评:此题属于二次函数综合题,涉及的知识有:待定系数法求抛物线解析式,平行四边形的性质,相似三角形的判定与性质,利用了数形结合及分类讨论的思想,分类讨论时注意考虑问题要全面.

练习册系列答案
相关题目
 点.
点. 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0). (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.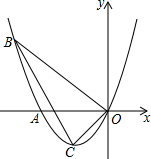 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.