题目内容
【题目】如图，△ABC为等边三角形，点D，E分别在AC，BC上，且AD＝CE，AE与BD相交于点P，BF⊥AE于点F．若PF＝2，则BP＝（ ）
A. 3 B. 4 C. 5 D. 6
【答案】B
【解析】
首先证△ABD≌△CAE，推出∠ABD=∠CAE，求出∠BPF=∠APD=60°，得出∠PBF=30°，根据含30度角的直角三角形性质求出BP=2PF即可．
∵△ABC是等边三角形，.
∴AB=AC，.
∠BAC=∠C，.
在△ABD和△CAE中，
，.
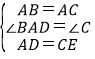∴△ABD≌△CAE，.
∴∠ABD=∠CAE，.
∴∠APD=∠ABP+∠PAB=∠BAC=60°，.
∴∠BPF=∠APD=60°，.
在Rt△BFP中，∠PBF=30°，.
∴BP=2PF，
∵PF=2，
∴BP=4.
故选B.
【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资，甲、乙两仓库分别有8吨、7吨防寒物资．从甲、乙两仓库运送防寒物资到A、B两地的运费单价（元／吨）如表1，设从甲仓库运送到A地的防寒物资为x吨（如表2）．
表1
甲仓库 | 乙仓库 | |
A地 | 80 | 100 |
B地 | 60 | 40 |
表2
甲仓库 | 乙仓库 | |
A地 | 10－x | |
B地 |
（1）完成表2；
（2）求运送的总运费y（元）与x（吨）之间的函数表达式，并直接写出x的取值范围；
（3）求最低总运费．
【题目】百年大计，教育为本.为了让贫困地区的孩子也能接受公平、有质量的教育，某中学学生积极响应号召，计划向某山区贫困中小学生进行捐助，捐助总人数为23名．资助一名中学生的学习费用需
元，一名小学生的学习费用需
元，初中各年级学生捐款数额与其恰好捐助贫困中学生和小学生人数的部分情况如下表：
年级 | 捐款数额（元） | 捐助贫困中学生人数（名） | 捐助贫困小学生人数（名） |
初一年级 | 4000 | 2 | 4 |
初二年级 | 4200 | 3 | 3 |
初三年级 | 7400 |
（1）求
的值；
（2）初三学生的全部捐款用于解决余下（部分或全部）的贫困中小学生的学习费用，求初三年级学生可捐助的贫困中、小学生人数．
