题目内容
 如图:直角梯形ABCD中,AD∥BC,AD<BC,∠B=90°,AB=7,BC-AD=1.以CD为直径的圆O与AB有两个不同的公共点E、F,与BC交于点G.
如图:直角梯形ABCD中,AD∥BC,AD<BC,∠B=90°,AB=7,BC-AD=1.以CD为直径的圆O与AB有两个不同的公共点E、F,与BC交于点G.(1)求⊙O的半径;
(2)求证:AE=BF;
(3)当AE=1时,在线段AB上是否存在点P,以点A,P,D为顶点的三角形与以点B,P,C为顶点的三角形相似?若存在,在图中描出所有满足条件的点P的位置(不要求计算);若不存在,请说理由.
(4)当AE为何值时,能满足(3)中条件的点P有且只有两个?
分析:(1)连接DG,根据直径所对的圆周角是直角得出DG⊥BC,在△DGC中根据勾股定理求出DC的长即可;
(2)作OM⊥AB于M,根据垂径定理求出EM=FM,根据梯形的中位线推出AM=BM即可;
(3)有三个点:①P与E重合时,∠CED=90°,根据同角的余角相等得出∠AED=∠ECB,又∠DAB=∠ABC,由两角对应相等的两三角形相似证明出△AED∽△BCE,即可求出AP;②P与点F重合时,与①类似能求出AP;③P在线段EF上,由△APD∽△BPC,根据相似三角形的性质得出比例式求出AP即可.
(4)当P3与E(P1)重合时,即∠AED=∠BEC=45°,只有两解,根据相似三角形的性质得出比例式求出AE=3.
(2)作OM⊥AB于M,根据垂径定理求出EM=FM,根据梯形的中位线推出AM=BM即可;
(3)有三个点:①P与E重合时,∠CED=90°,根据同角的余角相等得出∠AED=∠ECB,又∠DAB=∠ABC,由两角对应相等的两三角形相似证明出△AED∽△BCE,即可求出AP;②P与点F重合时,与①类似能求出AP;③P在线段EF上,由△APD∽△BPC,根据相似三角形的性质得出比例式求出AP即可.
(4)当P3与E(P1)重合时,即∠AED=∠BEC=45°,只有两解,根据相似三角形的性质得出比例式求出AE=3.
解答: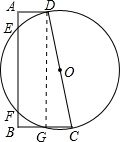 解:(1)连接DG.
解:(1)连接DG.
∵CD为直径,
∴DG⊥BC,
在△DGC中,∵BC-AD=1,
∴GC=1,
又∵AB=7,
∴DC=
=5
,
∴⊙O的半径为
;
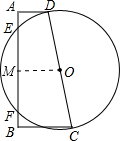 (2)作OM⊥AB于M,根据垂径定理得EM=FM,
(2)作OM⊥AB于M,根据垂径定理得EM=FM,
又∵AD∥OM∥BC,OD=DC,
∴AM=BM,
∴AM-EM=BM-FM,
即AE=BF;
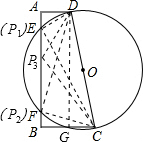 (3)有三个点.
(3)有三个点.
设AD=x,则BC=x+1,根据勾股定理,
AD2+AE2=DE2,即 x2+1=DE2,
BE2+BC2=CE2,即62+(x+1)2=CE2,
又CE2+DE2=CD2=50,
即 x2+1+[62+(x+1)2]=50,
解得 x=2,
即AD=2,BC=3.
第一种情况:∠APD+∠BPC=90.
只有∠DPC=90度时,∠APD+∠BPC=90,△PAD∽△CBP.
根据圆的特性,CD为直径,所以这样的点都在圆弧上,即点E,F
设AF=y.则根据AD2+AF2+BF2+BC2=CD2,
∴4+y2+(7-y)2+9=50,
解得y1=1,y2=6
即 AP=1,或者AP=6;
第二种情况:∠APD=∠BPC时,三角形PAD相似于PBC.
假设存在这样的点P,使得:∠APD=∠BPC时,△APD∽△BPC,则
AP:BP=AD:BC=2:3,
又∵AP+BP=AB=7,
所以AP=7×
=
.
综合以上,可以看出,这样的点有3个,AP的长度分别为 1,6,
;
(4)当P3与E(P1)重合时,即∠AED=∠BEC=45°,此时△APD与△BPC都是等腰直角三角形,
由△APD∽△BPC,得AP=AD,BP=BC,
又AP+BP=7,BC-AD=1,
∴AP=3,即AE=3.
故当AE=3时,满足(3)中条件的点P有且只有两个,即点E、点F.
 解:(1)连接DG.
解:(1)连接DG.∵CD为直径,
∴DG⊥BC,
在△DGC中,∵BC-AD=1,
∴GC=1,
又∵AB=7,
∴DC=
| 72+12 |
| 2 |
∴⊙O的半径为
5
| ||
| 2 |
 (2)作OM⊥AB于M,根据垂径定理得EM=FM,
(2)作OM⊥AB于M,根据垂径定理得EM=FM,又∵AD∥OM∥BC,OD=DC,
∴AM=BM,
∴AM-EM=BM-FM,
即AE=BF;
 (3)有三个点.
(3)有三个点.设AD=x,则BC=x+1,根据勾股定理,
AD2+AE2=DE2,即 x2+1=DE2,
BE2+BC2=CE2,即62+(x+1)2=CE2,
又CE2+DE2=CD2=50,
即 x2+1+[62+(x+1)2]=50,
解得 x=2,
即AD=2,BC=3.
第一种情况:∠APD+∠BPC=90.
只有∠DPC=90度时,∠APD+∠BPC=90,△PAD∽△CBP.
根据圆的特性,CD为直径,所以这样的点都在圆弧上,即点E,F
设AF=y.则根据AD2+AF2+BF2+BC2=CD2,
∴4+y2+(7-y)2+9=50,
解得y1=1,y2=6
即 AP=1,或者AP=6;
第二种情况:∠APD=∠BPC时,三角形PAD相似于PBC.
假设存在这样的点P,使得:∠APD=∠BPC时,△APD∽△BPC,则
AP:BP=AD:BC=2:3,
又∵AP+BP=AB=7,
所以AP=7×
| 2 |
| 5 |
| 14 |
| 5 |
综合以上,可以看出,这样的点有3个,AP的长度分别为 1,6,
| 14 |
| 5 |
(4)当P3与E(P1)重合时,即∠AED=∠BEC=45°,此时△APD与△BPC都是等腰直角三角形,
由△APD∽△BPC,得AP=AD,BP=BC,
又AP+BP=7,BC-AD=1,
∴AP=3,即AE=3.
故当AE=3时,满足(3)中条件的点P有且只有两个,即点E、点F.
点评:本题考查了圆周角定理,垂径定理,相似三角形的判定与性质,勾股定理等知识,综合性较强,有一定难度.进行分类讨论是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF. ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.