题目内容
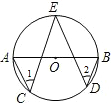 (2013•密云县二模)如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=
(2013•密云县二模)如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2=90°
90°
.分析:首先连接OE,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可得∠1=
∠AOE,∠2=
∠BOE,即可得∠1+∠2=
(∠AOE+∠BOE),则可求得∠1+∠2的度数.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: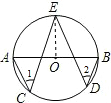 解:连接OE,
解:连接OE,
∵∠1=
∠AOE,∠2=
∠BOE,
∴∠1+∠2=
∠AOE+
∠BOE=
(∠AOE+∠BOE)=
×180°=90°.
故答案为:90°.
 解:连接OE,
解:连接OE,∵∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:90°.
点评:此题考查了圆周角定理.此题难度不大,注意准确作出辅助线是解此题的关键,注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目