题目内容
如图,在平面直角坐标系xOy中,抛物线 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?
(1)点B的坐标为(0,2);(2)DE=4;(3)m的值为8或-8..
解析试题分析:(1)将m=2代入原式,得到二次函数的顶点式,据此即可求出B点的坐标;
(2)延长EA,交y轴于点F,证出△AFC≌△AED,进而证出△ABF∽△DAE,利用相似三角形的性质,求出DE=4;
(3)①根据点A和点B的坐标,得到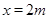 ,
,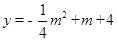 ,将
,将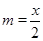 代入
代入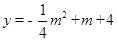 ,即可求出二次函数的表达式;
,即可求出二次函数的表达式;
②作PQ⊥DE于点Q,则△DPQ≌△BAF,然后分(如图1)和(图2)两种情况解答.
试题解析:(1)当m=2时,y=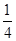 (x-2)2+1,
(x-2)2+1,
把x=0代入y=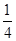 (x-2)2+1,得:y=2,
(x-2)2+1,得:y=2,
∴点B的坐标为(0,2).
(2)延长EA,交y轴于点F,
∵AD=AC,∠AFC=∠AED=90°,∠CAF=∠DAE,
∴△AFC≌△AED,
∴AF=AE,
∵点A(m,-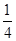 m2+m),点B(0,m),
m2+m),点B(0,m),
∴AF=AE=|m|,BF=m-(-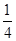 m2+m)=
m2+m)=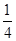 m2,
m2,
∵∠ABF=90°-∠BAF=∠DAE,∠AFB=∠DEA=90°,
∴△ABF∽△DAE,
∴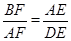 ,
,
即: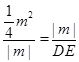 ,
,
∴DE=4.
(3)①∵点A的坐标为(m,-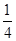 m2+m),
m2+m),
∴点D的坐标为(2m,-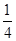 m2+m+4),
m2+m+4),
∴x=2m,y=-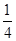 m2+m+4,
m2+m+4,
∴y=-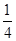 •(
•(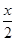 )2+
)2+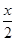 +4,
+4,
∴所求函数的解析式为:y=-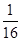 x2+
x2+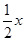 +4,
+4,
②作PQ⊥DE于点Q,则△DPQ≌△BAF,
(Ⅰ)当四边形ABDP为平行四边形时(如图1),
点P的横坐标为3m,点P的纵坐标为:(-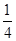 m2+m+4)-(
m2+m+4)-(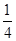 m2)=-
m2)=-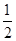 m2+m+4,
m2+m+4,
把P(3m,-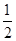 m2+m+4)的坐标代入y=-
m2+m+4)的坐标代入y=-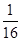 x2+
x2+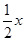 +4得:-
+4得:-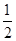 m2+m+4=-
m2+m+4=-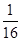 ×(3m)2+
×(3m)2+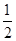 ×(3m)+4,
×(3m)+4,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=8.
(Ⅱ)当四边形ABPD为平行四边形时(如图2),
点P的横坐标为m,点P的纵坐标为:(-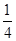 m2+m+4)+(
m2+m+4)+(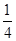 m2)=m+4,
m2)=m+4,
把P(m,m+4)的坐标代入y=-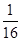 x2+
x2+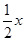 +4得:
+4得:
m+4=-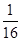 m2+
m2+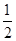 m+4,
m+4,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=-8,
综上所述:m的值为8或-8.
考点:二次函数综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD. AC时,求CE的长.
AC时,求CE的长.
 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
 的图象与反比例函数
的图象与反比例函数 图象的两个交点.
图象的两个交点.
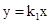 的图象于反比例函数
的图象于反比例函数 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式。
 的图象与一次函数
的图象与一次函数 的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.
的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.

 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .