题目内容
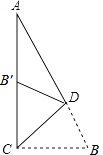
【题目】如图,某测量员测量公园内一棵树DE的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B、C、E三点在同一条直线上.
),且B、C、E三点在同一条直线上. 
(1)求斜坡AC的长;
(2)请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
【答案】
(1)解:如图,过点A作AF⊥DE于F,
则四边形ABEF为矩形,
∴AF=BE,EF=AB=3米,
设DE=x,
在Rt△CDE中,CE= ![]() =
= ![]() x,
x,
在Rt△ABC中,
∵ ![]() =
= ![]() ,AB=3,
,AB=3,
∴BC=3 ![]() ,
,
AC= ![]() =
= ![]() =6(米)\
=6(米)\

(2)解:在Rt△AFD中,DF=DE﹣EF=x﹣3,
∴AF= ![]() =
= ![]() (x﹣3),
(x﹣3),
∵AF=BE=BC+CE,
∴ ![]() (x﹣3)=3
(x﹣3)=3 ![]() +
+ ![]() x,
x,
解得x=9.
答:树高为9米
【解析】过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

练习册系列答案
相关题目