题目内容
【题目】如图,抛物线交X轴于A、B两点,交Y轴于点C ,![]() .
.
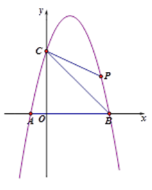
(1)求抛物线的解析式;
(2)平面内是否存在一点P,使以A,B,C,P为顶点的四边形为平行四边形,若存在直接写出P的坐标,若不存在请说明理由。
【答案】(1)![]() ;(2) (3,-4) 或(5,4)或(-5,4)
;(2) (3,-4) 或(5,4)或(-5,4)
【解析】
(1)设|OA|=1,确定A,B,C三点坐标,然后用待定系数法即可完成;
(2)先画出存在的点,然后通过平移和计算确定坐标;
解:(1)设|OA|=1,则A(-1,0),B(4,0)C(0,4)
设抛物线的解析式为y=ax2+bx+c
则有: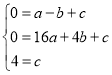 解得
解得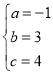
所以函数解析式为:![]()
(2)存在,(3,-4) 或(5,4)或(-5,4)
理由如下:如图:
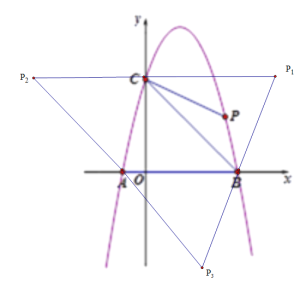
P1相当于C点向右平移了5个单位长度,则坐标为(5,4);
P2相当于C点向左平移了5个单位长度,则坐标为(-5,4);
设P3坐标为(m,n)在第四象限,要使A P3BC是平行四边形,
则有A P3=BC, B P3=AC
∴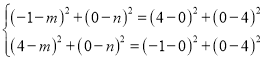 即
即![]() (舍去)
(舍去)![]()
P3坐标为(3,-4)

【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.